Gaussian中用TDDFT计算激发态和吸收、荧光、磷光光谱的方法
Gaussian中用TDDFT计算激发态和吸收、荧光、磷光光谱的方法
Method for calculating excited states and absorption, fluorescence, and phosphorescence spectra using TDDFT in Gaussian
文/Sobereva @北京科音
First release: 2015-Dec-22 Last update: 2024-Feb-19
1 前言
含时密度泛函理论(TDDFT)是当下最主流的电子激发问题的计算方法。本文专门介绍一下怎么用最流行的量子化学程序Gaussian做TDDFT计算得到电子激发相关的信息,以及结合Multiwfn程序得到电子吸收、荧光、磷光光谱。限于篇幅和笔者的时间,本文不可能把原理讲得很细,但只要理解本文介绍的基本原理,严格follow本文的例子,对自己研究的体系正确做计算一般是不成问题的。如果想完整、全面、系统学习电子激发相关的理论背景知识和对各种实际问题的计算方法,非常推荐零基础初学者们参加我讲授的北京科音初级量子化学培训班(http://www.keinsci.com/workshop/KEQC_content.html),对于已经有一定基础的人非常推荐参加讲得明显更深入、传授更多经验技巧的北京科音基础(中级)量子化学培训班(http://www.keinsci.com/workshop/KBQC_content.html),培训里有针对不同问题研究的巨量实例,讲的东西远远比本文多。另外在北京科音CP2K第一性原理计算培训班(http://www.keinsci.com/workshop/KFP_content.html)里我还会着重讲授用强大、免费、高效的第一性原理程序CP2K通过TDDFT做周期性体系电子激发研究的方法。
以下是一些相关资料,下面这三篇没看过的话一定要看看
使用Multiwfn绘制红外、拉曼、UV-Vis、ECD、VCD和ROA光谱图 http://sobereva.com/224
乱谈激发态的计算方法 http://sobereva.com/265
Multiwfn支持的电子激发分析方法一览 http://sobereva.com/437
我写的以下跟激发态研究有关的博文也很推荐一看
图解电子激发的分类 http://sobereva.com/284
使用Multiwfn便利地查看所有激发态中的主要轨道跃迁贡献 http://sobereva.com/529
电子激发任务中轨道跃迁贡献的计算 http://sobereva.com/230
使用Multiwfn做空穴-电子分析全面考察电子激发特征 http://sobereva.com/434
使用Multiwfn绘制跃迁密度矩阵和电荷转移矩阵考察电子激发特征 http://sobereva.com/436
在Multiwfn中通过IFCT方法计算电子激发过程中任意片段间的电子转移量 http://sobereva.com/433
使用Multiwfn绘制电荷转移光谱(CTS)直观分析电子光谱内在特征 http://sobereva.com/628
使用Multiwfn绘制构象权重平均的光谱 http://sobereva.com/383
使用Multiwfn计算特定方向的UV-Vis吸收光谱 http://sobereva.com/648
使用Multiwfn做自然跃迁轨道(NTO)分析 http://sobereva.com/377
在Multiwfn中基于fch产生自然轨道的方法与激发态波函数、自旋自然轨道分析实例 http://sobereva.com/403
使用Multiwfn考察轨道间重叠程度和质心距离 http://sobereva.com/371
电子激发过程中片段间电荷转移百分比的计算 http://sobereva.com/398
通过量子化学计算和Multiwfn程序预测化学物质的颜色 http://sobereva.com/662
使用Multiwfn计算odd electron density考察激发态单电子分布 http://sobereva.com/583
振动分辨的电子光谱的计算 http://sobereva.com/223
谈谈势能面交叉对激发态优化的影响 http://sobereva.com/468
基于背景电荷计算分子在晶体环境中的吸收光谱 http://sobereva.com/579
使用ORCA在TDDFT下计算旋轨耦合矩阵元和绘制旋轨耦合校正的UV-Vis光谱 http://sobereva.com/462
使用CP2K结合Multiwfn对周期性体系模拟UV-Vis光谱和考察电子激发态 http://sobereva.com/634
使用Dalton通过CC3方法极高精度计算激发态 http://sobereva.com/693
CIS、TDDFT计算的CT激发能随CT距离的渐进行为的总结 http://sobereva.com/321
另外也建议读一下这篇入门级综述文章,会有帮助:Chem. Soc. Rev., 42, 845-856 (2013)。文中的说法凡是和本文有冲突的,一律以本文为准。
下文第2节先介绍一下基础知识,第3节介绍TDDFT计算涉及到的关键词,第4节给出一些例子。
2 原理
2.1 理论方法
各种计算激发态的方法,比如CIS、TDDFT、TDHF、ZINDO、EOM-CCSD、SAC-CI、LR-CC3、CASPT2等等,直接给出的都是在某个结构下,基态与各个激发态之间的电子能量差。这些方法也可以优化激发态和对激发态做振动分析,也能给出激发态波函数信息用于讨论激发态原子电荷、偶极矩、电子定域性等问题。目前最流行的用得最多的是TDDFT,达到了精度与效率的较好平衡点。但TDDFT计算精度严重依赖于泛函,必须根据体系特征、激发类型选择合适的泛函才能得到不错结果。至于基组,若泛函选择得当,对于大体系用6-31G*就能得到定性正确结果,如果计算量尚有余裕想改进定量精度,建议用def-TZVP(Gaussian里直接写为TZVP)。若计算里德堡激发,则必须有弥散函数,至少aug-cc-pVDZ。泛函和基组的选择的详细讨论见前述的《乱谈激发态的计算方法》,判断激发类型的方法见前述的《图解电子激发的分类》。
2.2 电子跃迁过程
实际上,吸收、发射过程既涉及到电子态的改变也涉及到振动态的改变,完整考虑这样的过程比较麻烦,需要优化基态结构、对基态做振动分析、优化激发态结构(挺耗时)、对激发态做振动分析(巨耗时)。
为了简化计算和讨论,人们一般忽略核振动的量子效应,只考虑电子势能面。此时电子跃迁可用以下假想模型表示:
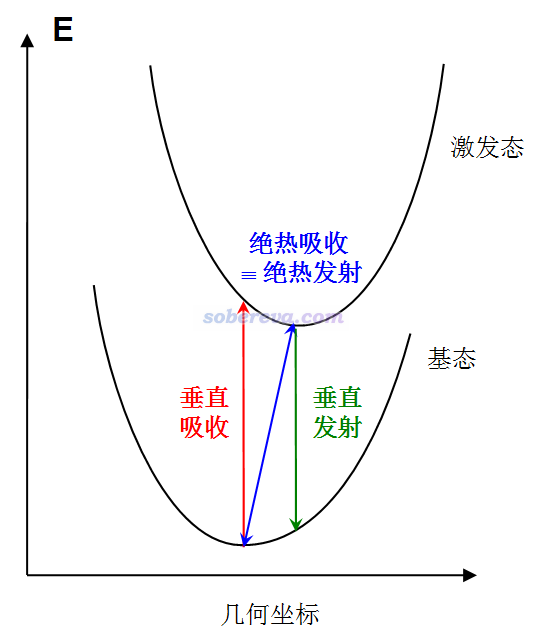
我们一般研究激发态计算的是以下三种理想化的跃迁方式:
(1)垂直吸收:电子从基态吸收光子而被激发到激发态,结构保持基态的极小点结构。计算垂直吸收能包含以下两步
1.优化基态几何结构
2.在1的结构下计算基态到感兴趣的激发态的激发能
(2)垂直发射:电子从激发态发射光子而退激到基态,结构保持激发态的极小点结构。计算垂直发射能包含以下两步
1.优化激发态几何结构(初猜结构无所谓,如果不知道激发态结构什么样,一般用基态极小点结构作为初猜结构)
2.在1的结构下计算基态到激发态的激发能(这便是这个激发态垂直发射到基态的能量)
(3)绝热吸收:电子从基态被激发到激发态,结构也从基态极小点结构变化到激发态极小点结构。计算绝热吸收能包含以下三步
1.优化基态几何结构,在最后一步得到基态极小点能量
2.优化激发态几何结构,在最后一步得到激发态极小点能量
3.将第二步得到的能量与第一步得到的能量求差值
绝热发射是绝热吸收的逆过程,跃迁能量相同。
以上跃迁方式是理想化的,对理论研究有用,对于研究实际问题也有用。实际吸收、发射光谱的最大峰位置一般分别比较接近于垂直吸收能和垂直发射能。而0-0跃迁,即两个电子态的振动基态间的跃迁能,比较接近于绝热激发能。
基态是单重态(S0)时,发射过程又分为两类:
(1)荧光发射:是从单重态激发态发射光子退激到基态。根据kasha规则,荧光发射多数情况是从S1(能量最低的单重态激发态)退激到S0。因此,按照上述垂直发射方式计算荧光的时候,激发态一般选的是S1态。少数情况kasha规则不满足,比如Azulene大多是从S2而非S1退激到S0的。
(2)磷光发射:是从三重态激发态发射光子退激到基态。磷光发射是从T1(能量最低的三重态激发态)退激到S0的。因此,按照上述垂直发射方式计算磷光的时候,激发态选的是T1态。
2.3 跃迁电偶极矩与振子强度
假设初始态电子波函数为|i>,末态为|j>,则两个态之间的跃迁电偶极矩为<i|-r|j>。这里r是坐标矢量,负号是因为电子带负电荷。跃迁偶极矩一般指的就是跃迁电偶极矩,但也有跃迁磁偶极矩、跃迁速度偶极矩等等。注意,跃迁电偶极矩和两个态之间电偶极矩的差值,即<j|-r|j>-<i|-r|i>,根本没直接关系,很多初学者都搞混了。
有了跃迁电偶极矩和两个态能量差ΔE,就能得到两个态之间跃迁对应的振子强度f:(2/3)ΔE*|<i|-r|j>|^2,是个无量纲的量。
基态体系与某个激发态之间的振子强度越大,就越容易吸收相应频率的电磁波而跃迁到那个激发态上,因此吸收光谱中相应的吸收峰也越强。一般情况下振子强度小于1,但也完全可以大于1,极强吸收峰的振子强度甚至能达到接近7、8。振子强度小于0.01一般可以认为跃迁禁阻。
通过振子强度和两个态之间的能量差就可以根据爱因斯坦公式计算激发态寿命,对于荧光和磷光发射都适用,往往和实验对应得不错。如果和实验值差异很大,有可能发生了显著的内转换、外转换等无辐过程。计算公式为:寿命τ=1.5/(f*ΔE^2)。这里寿命的单位为秒,ΔE以cm-1为单位。寿命的倒数就是自发辐射速率。
三重态和单重态之间是自旋禁阻的,仅当考虑旋轨耦合时振子强度才不为零,但数值依然很小,所以磷光寿命远比荧光寿命长。
2.4 电子光谱的产生
激发能、振子强度都是纯粹的理论数据,要把它转化为能和实验对比的UV-Vis(紫外-可见吸收光谱)、荧光、磷光光谱,需要把跃迁进行展宽。这里简单说一下计算过程。
(1)UV-Vis光谱:在基态优化的结构下计算基态到一批激发态的激发能和振子强度,然后把每个跃迁根据这两个量用高斯函数展宽,再把所有跃迁进行叠加,即得到UV-Vis光谱图。Gaussian等程序还顺便输出基态到各激发态的转子强度,用它代替振子强度进行展宽的话得到的是电子圆二色谱(ECD)。
(2)荧光光谱:假设kasha规则是满足的,在优化的S1结构下计算S1->S0的垂直发射能以及对应的振子强度,然后用高斯函数展宽成峰形即是荧光光谱图。
(3)磷光光谱:在优化的T1结构下计算T1->S0的垂直发射能以及对应的振子强度(需考虑旋轨耦合,否则必为0),然后用高斯函数展宽成峰形即是磷光光谱图。
至于展宽的细节和实现,详见前述的《使用Multiwfn绘制红外、拉曼、UV-Vis、ECD和VCD光谱图》。
由于电子激发实际上还涉及到不同振动态之间的跃迁,所以电子光谱是有精细结构的(但在极性溶剂下观测不到,只能观测到带状光谱)。如果不考虑核振动,即用前面介绍的计算方式,得到的理论光谱是没有精细结构的,特别是荧光、磷光光谱图上仅仅只有一个高斯峰形而已。如果要得到含有精细结构的电子光谱,即振动分辨(Vibrationally-resolved)的电子光谱,必须考虑核振动波函数。具体做法见前述的《振动分辨的电子光谱的计算》。算这个的成本比前述不考虑核振动效应时高得多。
2.5 溶剂效应
溶剂效应对激发态的影响有多方面,会影响激发能而导致谱峰位移,还会影响吸收/发射的强度、使谱峰加宽和变形、影响激发态结构、出现外转换而退激等等。凡是实际是在溶液中发生的和电子激发有关的问题,计算时应当考虑溶剂,溶剂极性越强考虑的必要性越大。
量化计算激发能的时候一般都是用隐式溶剂模型,将溶剂环境当成具有一定介电常数的连续介质来考虑。这种方式考虑溶剂效应一般可以基本合理表现出它对激发能、振子强度的影响以及对激发态结构的影响。隐式溶剂模型种类很多,激发态计算的目的一般就用PCM,这也是Gaussian的SCRF关键词默认的,其它程序有的只支持比PCM形式更简单的COSMO,效果也差不多。
TDDFT级别下,隐式溶剂模型的溶剂场对激发态的响应有不同考虑方式。常用的有两种:
(1)线性响应(Linear response, LR):溶剂对激发能的修正量是跃迁密度与跃迁密度导致的溶剂极化之间的相互作用。这种处理比较常用,相比气相计算不会额外带来太多耗时。
(2)态特定(State-specific, SS):令溶剂直接对指定的激发态的密度进行响应,通过反复迭代令溶剂场与激发态密度间完全自洽。每次迭代都要做电子激发计算求出激发态密度,因而也称外迭代(External iteration)。这将使计算耗时增加一个数量级,还使得TDDFT失去解析梯度。因此仅当对结果要求精确的时候使用,且一般不用在优化激发态的过程中。而且一次只能考虑一个激发态,难以获得同时涉及很多态的吸收光谱。一般来说,除非考察的是电荷转移激发态,否则昂贵、麻烦的SS实际上并不比LR有多大优势,甚至还可能结果更差。
溶质会使溶剂分子被极化,包括溶剂的电子结构被极化以及分子朝向被极化,分别对应于溶剂弛豫的快部分和慢部分。对于处于某个电子态的体系,若溶剂的两部分都已经对其弛豫了,称为平衡溶剂(eq);如果只是快部分弛豫了,称为非平衡溶剂(neq)。垂直吸收、垂直发射的过程非常短暂,末态时溶剂分子只有其电子部分来得及被重新极化,而朝向来不及被重新极化还停留在初态的状况,因此初态计算时应处于平衡溶剂下,而末态计算时应处于非平衡溶剂下。绝热吸收/发射过程则可认为在初态和末态时溶剂都已完全弛豫,即都处在平衡溶剂下。在溶剂中计算吸收/发射能严格来说应当考虑非平衡溶剂效应(尽管是否考虑影响不很大),根据上面的讨论,计算方法如下所示
垂直吸收能 = E_ES(R_GS, neq) - E_GS(R_GS, eq)
垂直发射能 = E_ES(R_ES, eq) - E_GS(R_ES, neq)
绝热吸收能 = 绝热发射能 = E_ES(R_ES, eq) - E_GS(R_GS, eq)
其中E_ES和E_GS分别代表激发态和基态能量。R_ES和R_GS分别代表激发态极小点结构和基态极小点结构。诸如E_ES(R_GS, neq)的含义就是在基态极小点结构下、非平衡溶剂下的激发态能量。
是否考虑非平衡溶剂效应,用线性响应还是态特定方法,是不同类别的问题,可以以不同方式组合。原理上说,用态特定方法,同时考虑非平衡溶剂效应,得到的激发能是最准确的,但也最耗时、繁琐,Gaussian手册上那个“7步”例子之所以搞得那么麻烦,就是因为用了这种方式考虑溶剂,而且从吸收到发射算了一个完整来回,于是把初学者们搞晕了。如果不要求那么高,用线性响应模型其实就够了,由于误差抵消之类因素,也不一定比态特定的结果差,还省了大量时间。
3. Gaussian中的TDDFT计算
3.1 关键词
Gaussian中做TDDFT计算的关键词基本格式是“# 泛函/基组 TD(选项)”。激发态优化、振动分析、找过渡态、产生IRC、势能面扫描等依赖于势能面的任务对于激发态也照样可以做,关键词和基态时完全一致,比如要优化激发态就加个opt,要算激发态频率就加个freq。
TD里的常用选项有下
nstates=N:表明总共算能量最低的N个激发态的信息,如激发能、跃迁电/磁偶极矩、振子强度、组态系数等。默认为3。
root=i:选择感兴趣的态。如果当前任务是与某个激发态有关的,比如几何优化、振动分析、获得偶极矩等,则表明是对第i个激发态做的。只是计算激发态信息则不需要管此设定。默认为1。
singlet:要求计算的N个激发态都为单重态,此为默认。
triplet:要求计算的N个激发态都为三重态。
50-50:要求同时计算N个单重态和N个三重态。
注意singlet、triplet、50-50关键词只对基态是闭壳层有效,基态是开壳层的话,没法指定激发态的自旋多重度,而只能是算出什么态就是什么态,得根据激发态的<S**2>来判断激发态的自旋多重度。<S**2>的理想值为S(S+1),S是体系的自旋量子数。常见的几种情况如下:
单重态=0.0
二重态=0.75
三重态=2.0
四重态=3.75
五重态=6.0
...
因此,比如一个自由基,算出来某个激发态的<S**2>=0.85,相对来说比较接近于上表的0.75,因此可以认为是二重态激发态。
3.2 nstates的设置
原理上nstates越大结果越准确,但设得越大计算耗时越多,因此不能盲目设大。nstates应该设多大值得专门说一下,有两种情况:
(1)研究特定激发态的情况
除非有对称性,否则无论哪种激发态算法,都是按照激发能从低往高算的。即计算第i个激发态,就必须把能量小于i的激发态也算出来。所以,如果感兴趣的是第i个激发态,则总共需要计算至少i个激发态。
对于TDDFT,研究第i个激发态时不要恰好只算i个态,建议算到i+3个态,算到i+5个态更稳妥,比起只算i个态时第i个态的能量会更准确。因为Gaussian是通过Davidson迭代方式近似求解TDDFT方程来得到最低的一批解,其中最高的几个态的误差会比更低的态更大。但也没必要算的态数超过i太多,否则会浪费很多时间。
(2)计算电子光谱的情况,需要综合考虑三点问题:
波长范围(主要):对于同一个体系,算的态数越多,涉及的激发能范围就越高,得到的理论光谱因此就能覆盖到光谱图越低的波长。
体系(主要):若要算到同样的波长,体系共轭程度越大、杂原子越多,需要算越多的态。对于同类体系,原子数越多时需要算越多的态。
理论方法(次要):算到同样的波长,HF成份越高的泛函做TDDFT由于激发能整体越高,因此需要算越少的态。
通常计算光谱需要覆盖整个可见光区和部分UV区,一般感兴趣的是2~7eV区间。算多少态需要经验,往往还需要尝试(可以先用低级别的方法如ZINDO或小基组测试一下)。比如有的小体系可能算10个足矣,但一些共轭大分子体系往往要算上百乃至几百。态数算少了光谱范围覆盖不足需要重算,而算得太多则白算出来一堆能量过高的不感兴趣的激发态,这都会浪费大量时间。
Gaussian的TDDFT支持一个叫DEmin的关键词,当你发现态数设少了,想补算能量更高激发态的时候有一定用处,见《在Gaussian中对不同能量区间分批计算激发态》(http://sobereva.com/348)。
3.3 TDDFT的频率计算、过渡态和IRC计算
Gaussian09支持TDDFT的解析梯度,所以用TDDFT优化激发态速度不错,但是不支持解析的Hessian,必须基于解析梯度做一阶有限差分获得,因此做振动分析耗巨耗时,相当于6N步(N=原子数)几何优化的耗时,对于大点的体系很难算得动,因此应尽量避免用TDDFT做振动分析。但Gaussian09支持CIS的解析Hessian,因此如果对激发态频率、振动耦合的电子光谱精度要求不太高,在Gaussian中用CIS做振动分析足矣。找过渡态、走IRC众所周知需要提供初始的Hessian。然而,TDDFT下写calcfc计算初始的Hessian过于昂贵,因此在Gaussian09中找激发态的过渡态时建议用opt=(TS,modRedundant,noeigen)或者opt=(TS,gediis,noeigen),走IRC建议用建议用IRC(gradientonly,euler),这样就不需要用TDDFT通过有限差分计算昂贵的Hessian了,可惜这种方式走IRC的成功几率较低。
在Gaussian16中,已经支持TDDFT的解析Hessian了,因此对激发态找过渡态、走IRC都不需要什么特殊考虑,直接像对待基态一样写关键词就行了,只不过需要多写上TD而已,比如可以用# B3LYP/6-31G* TD(root=2,nstates=5) opt(TS,calcfc,noeigen)以当前结构为初猜结构找第2激发态上的过渡态。
3.4 激发态的波函数
默认情况下,做TDDFT计算的时候Gaussian产生的是基态的密度,即末尾输出的多极矩是基态的,波函数分析模块(L601)、NBO模块(L607)分析的也是基态波函数。TDDFT计算时如果同时写上density关键词,说明产生当前级别的密度,即root指定的激发态密度。这样多极矩、NBO分析、原子电荷等等都是对root指定的激发态计算的,输出的.wfn/.wfx文件里记录的也将是第root激发态的自然轨道。但此时chk里记录的轨道依然是基态的DFT轨道,如果要把激发态自然轨道转存到chk里需要多做一步,见Multiwfn手册第四章开头的说明或《详谈Multiwfn支持的输入文件类型、产生方法以及相互转换》(http://sobereva.com/379)。更简单的做法是直接通过Multiwfn基于fch里的激发态密度矩阵产生激发态自然轨道,见《在Multiwfn中基于fch产生自然轨道的方法与激发态波函数、自旋自然轨道分析实例》(http://sobereva.com/403)。
3.5 T1的优化
优化T1值得专门一说。有两种做法,一种是用UDFT(也叫UKS),即自旋多重度设3直接优化,不写TD关键词,比如0 3结合# PBE1PBE/6-31G* opt,这样是通过SCF方式直接算T1态并优化它,不牵扯TDDFT计算;另一种是自旋多重度设1同时用TD(triplet),比如0 1结合# PBE1PBE/6-31G* TD(triplet) opt,这样每一步就是先计算单重态基态作为参考态,再通过TDDFT计算T1态并优化它。这两种方式原理上都合理,结果通常相近,但强烈建议用UDFT方式,因为其耗时只比优化单重态基态增加一点,而用TDDFT优化T1的话计算量则要增加约一个数量级。
不过UDFT方法缺点是只能优化T1,而TDDFT则可以优化任意三重态激发态,而且能够同时给出轨道跃迁信息。
经常有初学者写成0 3结合TD(triplet) opt,这样算出来什么都不是,根本就不是优化T1。
3.6 溶剂模型
Gaussian里TDDFT计算时写上诸如SCRF=solvent=xxx就能在TDDFT计算时使用表现xxx溶剂的PCM溶剂模型。前面提到的线性响应(LR)和态特定(SS)方式都能支持,详情如下
线性响应模型(LR):是SCRF关键词默认的。对耗时增加不多,而且TDDFT依然有解析梯度,因此最适合激发态几何优化。但如前所述,对溶剂效应表现得相对粗略。
态特定(SS):需要在SCRF里面写ExternalIteration(等价于G09老版本中的statespecific),溶剂场会与root指定的激发态的密度迭代到自洽,虽然比LR更准但很耗时间,而且一次只能对一个激发态来做。SS还使得TDDFT没有解析梯度,因此SS基本没法用在激发态优化上。
考虑非平衡溶剂(neq)效应只是对垂直吸收、发射过程而言的,优化过程中应当使用平衡溶剂(eq),因为随着溶质结构的变化溶剂的朝向会同步变化。
Gaussian中使用LR的时候,在特定结构下计算激发态时,对激发态来说是非平衡溶剂(LR-neq),即溶剂慢部分对于基态是平衡的,只有快部分响应了激发态;在激发态几何优化时对激发态用的是平衡溶剂(LR-eq),即溶剂快慢部分都是对于激发态平衡的。计算中输出的基态能量总是在基态的平衡溶剂下的。
Gaussian中使用SS的时候,对激发态默认使用平衡溶剂(SS-eq)。基于SS计算激发态时,当默认的平衡/非平衡溶剂设定和实际情况不符时,需要在SCRF里写read关键词读取额外的溶剂设定,这些设定在输入文件末尾空一行后书写。在初态计算时用noneq=write来写入初态时溶剂慢部分的信息,然后在末态计算时再用noneq=read来读取初态溶剂慢部分的信息。
如果对溶剂模型还糊涂没关系,直接仔细follow后文的例子就行了,不用想太多。
4. 实例
下面的例子不拿具体体系为例,就只是把用的步骤和关键词介绍一下,一定要举一反三。用的泛函和基组是随便选的,示意一下而已。假设体系的基态是单重态。
4.1 气相下计算最低5个垂直激发能
1 基态几何优化:# PBE1PBE/6-31G* opt
2 取上一步优化得到的结构,#p PBE1PBE/TZVP TD(nstates=5)
输出文件中会看到以下输出,这些是基态到各个激发态的跃迁电、速度、磁偶极矩矢量,以及振子强度(Osc.)。Dip. S.是跃迁偶极矩各个分量平方和。
Ground to excited state transition electric dipole moments (Au):
state X Y Z Dip. S. Osc.
1 -0.1494 0.1449 -0.0654 0.0476 0.0062
2 -0.0829 0.0804 0.0707 0.0183 0.0030
3 0.3706 -0.0971 0.0232 0.1473 0.0252
4 0.3399 0.0539 -0.2128 0.1637 0.0305
5 -0.0200 -0.0149 -0.2283 0.0527 0.0101
Ground to excited state transition velocity dipole moments (Au):
state X Y Z Dip. S. Osc.
1 0.0368 -0.0331 0.0186 0.0028 0.0095
2 0.0436 -0.0233 -0.0285 0.0033 0.0089
3 -0.0787 0.0272 -0.0027 0.0069 0.0180
4 -0.1240 -0.0026 0.0725 0.0206 0.0492
5 -0.0070 -0.0017 0.0706 0.0050 0.0117
Ground to excited state transition magnetic dipole moments (Au):
state X Y Z
1 -0.3277 0.4784 0.1051
2 -0.0701 -0.7474 -0.6712
3 -0.2194 0.0764 -0.5296
4 0.2326 0.2713 0.0772
5 0.0186 0.0527 -0.0944
然后会输出速度表象下的转子强度R(velocity)以及长度表象下的转子强度R(length),绘制ECD才需要。
<0|del|b> * <b|rxdel|0> + <0|del|b> * <b|delr+rdel|0>
Rotatory Strengths (R) in cgs (10**-40 erg-esu-cm/Gauss)
state XX YY ZZ R(velocity) E-M Angle
1 -20.9390 -24.0915 -48.3977 -31.1427 146.38
2 42.4101 28.6271 25.4666 32.1679 54.36
3 3.9375 32.5287 20.8226 19.0963 64.44
4 -7.0182 -38.0949 -15.4724 -20.1952 117.12
5 -17.5879 0.1833 0.3918 -5.6709 152.16
1/2[<0|r|b>*<b|rxdel|0> + (<0|rxdel|b>*<b|r|0>)*]
Rotatory Strengths (R) in cgs (10**-40 erg-esu-cm/Gauss)
state XX YY ZZ R(length)
1 -34.6361 -49.0075 4.8628 -26.2603
2 -4.1120 42.4792 33.5736 23.9803
3 57.4977 5.2465 8.6921 23.8121
4 -55.9240 -10.3458 11.6247 -18.2150
5 0.2632 0.5565 -15.2443 -4.8082
然后输出各个激发态的信息,如下所示。从输出的第一激发态的信息中可知它是单重态,不可约表示是A,激发能是5.3393eV (232.21nm),振子强度是0.0062。E(TD-HF/TD-KS)后面的值是这个激发态的能量,即前面输出的SCF Done对应的基态能量加上这里输出的激发能。root设多少、设不设都不会影响激发能的输出,但是只有root选的激发态(此例没设,默认为1),程序才会直接将它的总能量输出出来。诸如23 -> 25 -0.20249这样的输出的含义看前面提到的《电子激发任务中轨道跃迁贡献的计算》就行了,这里不提了。
Excited State 1: Singlet-A 5.3393 eV 232.21 nm f=0.0062 <S**2>=0.000
23 -> 25 -0.20249
24 -> 25 0.67156
This state for optimization and/or second-order correction.
Total Energy, E(TD-HF/TD-KS) = -323.278949720
Copying the excited state density for this state as the 1-particle RhoCI density.
Excited State 2: Singlet-A 6.6806 eV 185.59 nm f=0.0030 <S**2>=0.000
23 -> 25 0.47726
24 -> 25 0.18113
24 -> 26 0.44412
24 -> 27 -0.16152
...略
值得一提的是,虽然nstates设了5,此例得到了5个态的激发能,但是如前所述,越高的态激发能越不准。因此如果确实要得到准确的5个最低的激发能,建议将nstates设为10。
之后,利用这个Gaussian输出文件,通过Multiwfn就可以绘制UV-Vis和ECD光谱了,详见前述的《使用Multiwfn绘制红外、拉曼、UV-Vis、ECD和VCD光谱图》。用gview也可以绘制,但是可调选项没有Multiwfn灵活,功能没有Multiwfn强大,还是收费的。
假设你要考察第i激发态的波函数信息(如偶极矩),并同时得到相应的wfn文件用于Multiwfn的分析,这样写关键词:#p PBE1PBE/TZVP TD(nstates=5,root=i) density out=wfn,然后末尾空一行写上wfn文件的输出路径。这个任务算完后输出文件末尾显示的偶极矩、四极矩,还有Mulliken电荷等等都是第i激发态的。如果比如还要对这个态做NBO分析,再写个pop=NBO就完了。
4.2 气相下计算某分子S1结构和荧光发射能
1 基态几何优化:# PBE1PBE/6-311g(d) opt (如果你觉得初始结构已经比较合理的话,这一步可以省)
2 取上一步优化得到的结构,做S1态优化:# PBE1PBE/6-311g(d) TD opt (TD默认是root=1,默认的nstates=3对于优化S1一般够了,所以这里只写个TD)
第二步最后的结构就是S1结构了。每一步优化都会做一次电子激发计算,所以会看到很多上一节那样的输出。最后一次输出的第一激发态的激发能就是荧光发射能了。
利用第二步的输出文件就可以绘制荧光光谱了。这里假定是符合kasha规则从S1发射的,所以绘图时要把一同输出的S2、S3的信息抹掉。如果用gview绘制,手动将S2、S3态的振子强度设为0,再按照绘制UV-Vis光谱操作即得到荧光光谱。若用Multiwfn绘制则不需要手动修改输出文件,将输出文件载入Multiwfn,依次输入以下命令即可
11 //绘制光谱图
3 //UV-Vis
20 //修改振子强度
2,3 //选择第2、3激发态
0 //振子强度设为0
0 //绘制光谱
如果你还有不明白的地方,看Multiwfn手册4.11.11节,里面有个完整的绘制BODIPY荧光光谱的例子。
顺带一提,如果你要优化S4,可以写比如# PBE1PBE/6-311g(d) TD(nstates=7,root=4) opt。
4.3 气相下计算T1结构和磷光发射能
有两种方法做这个事情。
方法一:
1 优化T1结构:# B3LYP/6-31G* opt,电荷和自旋多重度为0 3。
2 取上一步优化得到的结构,用# B3LYP/6-31G* TD(triplet),电荷和自旋多重度为0 1。第一激发态的激发能就是磷光发射能了。
方法二:
1 优化T1结构:# B3LYP/6-31G* opt,电荷和自旋多重度为0 3。取最后一步的能量,作为T1结构下T1能量。
2 取上一步优化得到的结构,0 1下用# B3LYP/6-31G*计算单点能,得到T1结构下S0能量。
3 将第1步的能量减去第2步的能量即是磷光发射能
虽然两个方法结果有定量差异,但原理上都对,由于方法二还考虑了轨道弛豫,所以原则上会更精确一些,而且由于不用做TDDFT计算所以耗时短,缺点是没法像方法一那样得到轨道跃迁信息。另外,如果你还用TDDFT算了荧光,那么建议用方法一算磷光,这样都在TDDFT下计算结果更有可比性。
由于Gaussian不支持TDDFT级别下的旋轨耦合计算,所以得不到磷光发射对应的振子强度(输出的数值为0),因此没法绘制磷光光谱、计算磷光速率。支持MCSCF、MRCI等级别下做旋轨耦合的程序不少,不过这类方法很难用于大体系。目前支持TDDFT下考虑旋轨耦合得到振子强度的程序不算多,只有ADF(巨贵而且坑爹,别买)、Dalton(免费,推荐使用,计算例子见http://bbs.keinsci.com/thread-2455-1-1.html,以及计算化学公社量子化学版里面Dalton分类的帖子),以及Dirac等支持二/四分量相对论TDDFT的程序(使用门槛略高)。如果你只需要计算单-三重态间的旋轨耦合矩阵元的话,可以将Gaussian与PySOC结合使用,见《使用Gaussian+PySOC在TDDFT下计算旋轨耦合矩阵元》(http://sobereva.com/411)。更好、更方便的选择是用ORCA,见《使用ORCA在TDDFT下计算旋轨耦合矩阵元和绘制旋轨耦合校正的UV-Vis光谱》(http://sobereva.com/462)。
4.4 基于线性响应溶剂模型做TDDFT计算
这个例子包含4个任务,你需要研究什么问题就follow哪个,没有顺序关系。此例是通过线性响应方法,通过PCM溶剂模型表现乙醇环境。
(1)溶剂下基态几何结构优化:# PBE1PBE/6-311G* opt scrf=solvent=ethanol
(2)计算溶液中的最低20个态的激发能。取(1)得到的结构,用这些关键词:# PBE1PBE/6-311G* TD(nstates=20) scrf=solvent=ethanol。然后如4.1节所说用Multiwfn或gview绘图可以得到溶剂下的吸收谱。
(3)优化溶液中的S1结构:取(1)得到的结构,用这些关键词:# PBE1PBE/6-311G* TD scrf=solvent=ethanol opt
(4)计算溶液中的荧光发射能:直接取(3)输出文件当中最后一次的S0->S1激发能即可。可以如4.2节所说用Multiwfn或gview绘制溶剂下的荧光谱(这里强调一点,获得荧光发射能不要取(3)的结构再单独做一次电子激发计算得到S0->S1的能量,因为此时激发态处于非平衡溶剂,和发射光谱的溶剂实际特征恰相反。如果你就是要取(3)的结构单独做一次电子激发计算,比如想使用比优化激发态更大的基组算发射能,那么可以在TD里加上Eqsolv,此时溶剂对激发态是平衡的,和实际发射的情况一致)。
如果要算磷光发射,把(3)改为用UDFT方式优化T1,然后在(4)中把TD里写上triplet即可。
可见,基于线性响应模型做TDDFT计算和气相下区别仅仅在于加上SCRF关键词而已,什么其它区别都没有,计算耗时也增加不多,十分省事。但如果非要用原理上更准确的特定态模型,那么如下一节所示,就繁琐多也慢多了。
4.5 基于特定态溶剂模型做TDDFT计算
这个例子包含4个任务,你需要研究什么问题就follow哪个,没有顺序关系。此例是通过特定态方法,靠PCM溶剂模型表现乙醇环境。
(1)溶剂下基态几何结构优化:和4.4节的(1)等同。
(2)计算溶液中基态到S1态的激发能:
特定态方法计算激发能时,默认情况下激发态处于平衡溶剂下,但实际中应当处于非平衡溶剂下(慢部分对基态是平衡的),因此需要做两步才能正确表现非平衡溶剂效应
第一步:在(1)得到的结构下,先在溶剂下做基态单点计算,把基态的溶剂信息写到chk里,同时得到基态在平衡溶剂下的能量(SCF Done后面的值):
# PBE1PBE/6-311G* scrf(read,solvent=ethanol),末尾空一行写noneq=write
第二步:做电子激发计算,并读取上一步在chk里写入的基态溶剂信息,由此得到激发态在非平衡溶剂下的能量:
# PBE1PBE/6-311G* TD scrf(externaliteration,read,solvent=ethanol) geom=check guess=read,末尾空一行写noneq=read
这一步计算耗时会很长,会反复计算许多次激发态,这是为了让溶剂场与S1态电子密度相互自洽(即外迭代过程)。输出文件末尾的下面这条信息告诉了你特定态方法+非平衡溶剂下的激发态的能量:
After PCM corrections, the energy is -153.527526510 a.u.
将这个能量减去第一步的能量就是所需的激发能了。
(3)优化溶液中的S1结构:和4.4节的(3)等同。特定态方法下虽然也能做几何优化,但巨慢,所以优化激发态还是应当用线性响应模型。
(4)计算溶液中的荧光发射能:
第一步:在(3)得到的结构下,获得平衡溶剂下的激发态能量,并将激发态溶剂信息写入chk:
# PBE1PBE/6-311G* TD scrf(externaliteration,read,solvent=ethanol),末尾空一行写noneq=write
激发态能量应当取末尾输出的After PCM corrections后面的能量值。
第二步:做基态计算,读取第上一步在chk里写入的激发态溶剂信息,得到非平衡溶剂下的基态能量(SCF Done后面的值):
#P PBE1PBE/6-311G* scrf(read,solvent=ethanol) geom=check guess=read,末尾空一行写noneq=read
然后将第一步的能量减去第二步的能量就是荧光发射能。
可见,用特定态方法比用线性响应方法繁琐得多也耗时得多。这一节涉及的激发态是S1态,如果考察第i激发态就把TD里面写上root=i即可。如果要算磷光发射,把(3)改为用UDFT方式优化T1,然后在(4)中把TD里写上triplet即可。
5 其它问题
有几个问题值得在这里说一下。5.1 注意优化激发态时破坏对称性
就是激发态和基态的对称性往往是不同的,优化小分子激发态的时候不注意这一点往往得不到真正的激发态极小点结构。例如乙醛,基态是Cs对称性,但是S1的极小点结构并不具有Cs对称性。因此,直接拿它的基态结构作为初始结构来优化S1是万万不可的,否则得到的S1结构会依然保持Cs对称性,做振动分析会发现虚频。为得到真正极小点结构,应当在优化S1前先把基态的结构人为地扭曲一下使得Cs对称性被破坏,比如随意微微扭动一个二面角。激发态对称性往往低于基态,所以如果基态有对称性,建议激发态优化前都先人为地稍微破坏一下对称性。5.2 注意构象问题
柔性分子有诸多构象,不同构象对应的吸收光谱也不一样,而且可能差异明显(特别是对构象敏感的ECD谱)。计算吸收光谱时,如果用的构象不是能量最低的构象,那么可能和实验谱差很多。Molclus(http://www.keinsci.com/research/molclus.html)是我开发的很方便易用而且免费的构象搜索程序,非常推荐用于构象搜索目的。如果Molclus搜索出来的多个构象能量相差不太大,而且彼此间在实验温度下足矣越过势垒能够相互转化,而且这些构象下的光谱差异不小,那么必须计算各自的波尔兹曼分布对光谱做权重平均,权重的计算方法见《根据Boltzmann分布计算分子不同构象所占比例》(http://sobereva.com/165),权重平均的光谱绘制见《使用Multiwfn绘制构象权重平均的光谱》(http://sobereva.com/383)。
5.3 激发能算出来是负值怎么办?
有的时候算出来的一个或多个激发能为负值,这说明SCF部分产生的参考波函数(即HF或DFT波函数)不是当前结构下真正的基态波函数,此时得到的激发能也没有意义。此时若用stable关键词进行波函数稳定性检测,一定会也提示波函数不稳定,解决方法:
先检查自旋多重度设定的合理性,看是否自旋多重度设定的和当前结构下实际基态波函数不符(比如当前结构下基态是单重态但却误设了三重态)。
若确信自旋多重度没设错,则做一次单点计算,同时写stable=opt关键词让Gaussian自动找出真正的基态波函数,然后做激发态计算的时候写guess=read读取其作为初猜波函数。
按以上方式处理后,若激发能都为正说明没问题了。
5.4 怎么分析电子激发?
光是算算激发能、光谱,经常会显得研究很肤浅,完全没有在电子激发本质、特征层面上进行讨论。Multiwfn是电子激发分析非常强大同时也是十分好用的工具,电子激发的类型是什么、牵扯到了哪些片段/原子/原子轨道、电子激发时哪个片段向哪个片段转移了多少电子、电子激发导致的正负电荷分离程度如何、哪些分子片段或分子轨道对振子强度有关键性影响、电子激发导致成键特征发生了什么变化等等全部细节都可以用Multiwfn非常容易地分析得特别透彻。以后经常做电子激发计算的读者务必要仔细看《Multiwfn支持的电子激发分析方法一览》(http://sobereva.com/437),此文有对电子激发分析手段十分全面的论述,熟练掌握后你会发现Multiwfn是电子激发研究完全离不开的工具。
5.5 注意势能面交叉对激发态优化的影响
激发态的能级分布往往很密集,彼此之间在很多结构下存在交叉,再加上激发态势能面有时候还有分叉之类特征,导致激发态的优化往往比基态的优化的情况复杂不少,比如会出现对不同激发态优化最终都优化到了相同结构,或者一开始优化的是比如S4态,但是发现在最终结构下这个态的能量却并不是第四低的。强烈建议读者在彻底掌握本文所述内容后阅读这篇文章:《谈谈势能面交叉对激发态优化的影响》(http://sobereva.com/468)。把这篇文章内容彻底搞明白了,对激发态优化时遇到的一些看似奇怪的现象就能理解到底是怎么回事了。