使用Multiwfn做空穴-电子分析全面考察电子激发特征
2022-Mar-1注:本文介绍的功能已支持结合CP2K做TDDFT计算研究周期性体系的电子激发,参见《使用CP2K结合Multiwfn对周期性体系模拟UV-Vis光谱和考察电子激发态》(http://sobereva.com/634)。
2025-Dec-7注:本文的例子是结合Gaussian演示的。结合ORCA做本文介绍的分析的方法见《Multiwfn结合ORCA的TDDFT计算做空穴-电子等分析的方法》(http://sobereva.com/758)。
使用Multiwfn做空穴-电子分析全面考察电子激发特征
Using Multiwfn to perform hole-electron analysis to fully investigate electronic excitation character
文/Sobereva @北京科音
First release: 2018-Aug-31 Last update: 2025-Dec-7
1 前言
空穴-电子(hole-electron)分析是Multiwfn程序支持的一种非常强大、极为实用的考察电子激发特征的一套方法,它将电子激发过程描述为“空穴→电子”,从而可以以图形化的方式非常直观地考察电子从哪离开、到哪去,是局域激发、整体激发、电子转移激发还是杂化特征的激发。还可以定量考察电子转移距离、空穴与电子的分离程度、原子或片段对电子激发的贡献、空穴与电子的库仑吸引能等等。此分析可以用于CIS、TDHF、TDA-DFT和TDDFT方法做的电子激发任务。空穴-电子分析的最初灵感来自于笔者和同行钟成的讨论,并早在2013年就已经在Multiwfn中实现了,之后又经过不断完善和扩展。到2022年已经有几百篇已发表的SCI文章使用了空穴-电子分析,如Nature Catalysis, 6, 574 (2023), Nature Materials, 19, 1332 (2020)、J. Phys. Chem. Lett., 9, 4857 (2018)等,以及笔者发表的Phys. Chem. Chem. Phys., 24, 7466 (2022)(介绍见http://sobereva.com/640)、Chem. Eng. J., 515, 163236 (2025)(介绍见http://sobereva.com/742)等。在笔者不少博文里也涉及了空穴-电子分析,如《图解电子激发的分类》(http://sobereva.com/284)、《在Multiwfn中通过IFCT方法计算电子激发过程中任意片段间的电子转移量》(http://sobereva.com/433)等。
本文撰写的目的是系统性地介绍一下空穴-电子分析,使更多人能了解到此方法的重要性,并充分应用于自己的研究当中。凡是仔细、认真阅读本文的读者,必定会感受到空穴-电子分析的强大。即便之前已经长期使用空穴-电子分析的人也请仔细阅读本文,其中涉及了很多技巧,并介绍了空穴-电子分析框架在最新的Multiwfn中加入的各种新特征和相对于老版本的变动。笔者未来会专门写一篇介绍空穴-电子分析的论文发表,在此文发表之前,请务必在引用Multiwfn程序启动时提示的原文的同时也引用笔者的此文:Carbon, 165, 461-467 (2020) DOI: 10.1016/j.carbon.2020.05.023。在这篇文章中笔者应用了空穴-电子分析研究了18碳环体系,并且在补充材料里对空穴-电子分析的原理做了简要介绍,并与其它可以分析空穴、电子分布的方法做了对比。
除了空穴-电子分析外,本文对目前已经被不少文章使用的衡量电子激发特征的Λ和Δr指数的原理、与空穴-电子分析的关系以及在Multiwfn中的计算方法也作了介绍。看过本文后会明白这些指标已经没有什么存在价值了,完全可以被空穴-电子分析框架里定义的更好的指标所取代。
本文内容对应于Multiwfn官网上的最新版本,如果发现本文内容或情况和你手里的Multiwfn不符,请先更新至最新版本。Multiwfn可以在其主页http://sobereva.com/multiwfn上免费下载。如果不了解Multiwfn,强烈建议参看《Multiwfn入门tips》(http://sobereva.com/167)和《Multiwfn波函数分析程序的意义、功能与用途》(http://sobereva.com/184)。除本文介绍的方法外,Multiwfn还支持一大堆极具价值的激发态分析方法,在此文里有汇总介绍,很建议一看:《Multiwfn支持的电子激发分析方法一览》(http://sobereva.com/437)。
2 空穴-电子分析的原理
空穴-电子分析原理的详细介绍参看Multiwfn手册3.21.1.1节。本节只是做一些基本性的介绍,有看不明白的请结合手册看。
2.1 电子激发过程中空穴和电子的定义
对于CIS、TDHF、TDA-DFT和TDDFT,激发态波函数通过单激发组态函数的线性组合来描述,对这些方法不了解的话可参看《乱谈激发态的计算方法》(http://sobereva.com/265)。对于CIS和TDA-DFT,每个组态函数各有个系数w;对于TDHF、TDDFT,每个组态函数既可作为激发组态而拥有系数w,也可以作为去激发组态而拥有系数w',这点在Multiwfn手册3.21节开头特意介绍了。经过推导,对于TDHF/TDDFT,空穴和电子的表达式可写为以下形式。如果是CIS、TDA-DFT,则没有w'那部分。

上式中,r是坐标矢量,φ是轨道波函数,i或j是占据轨道标号,a或b是空轨道标号。因此诸如∑i→a代表循环每一个激发组态,而∑i←a代表循环每一个去激发组态。空穴分布ρhole和电子分布ρele都分为局域项(local term)和交叉项(cross term)两部分。局域项一般占主导,体现组态函数自身的贡献,而交叉项也不可忽略,否则定量不准,它体现组态函数之间的耦合对空穴和电子分布的影响。
“空穴”和“电子”这两个词并不是Multiwfn里的空穴-电子分析独创的,这两个词是抽象的概念,具体怎么定义并不唯一,应该说上面的这种定义是非常理想的,它满足合理的空穴、电子定义所理应满足的要求,即空穴和电子在全空间中积分值都为1(对应一个电子),而且处处为正。因此,上述方式定义的“空穴”的分布完美地描述了被激发的电子从哪里走,而“电子”的分布完美地描述被激发的那个电子去了哪。
实际上,倘若某个电子激发可以完美地由某一对轨道跃迁i→a所描述,换句话说这个组态函数的贡献恰为100%(怎么算贡献看《电子激发任务中轨道跃迁贡献的计算》http://sobereva.com/230),那么φi和φa就可以直接理想地分别作为空穴和电子。而上面方式定义的空穴和电子,则分别相当于|φi|^2和|φa|^2的,可以视为是i和a轨道对应的电子密度(假设这俩轨道都是单占据情况)。因此,上面定义的电子和空穴是没有相位信息的,因为对轨道波函数求了模方。由于实际算出来的电子激发态总是由很多组态函数共同参与,没有哪一对轨道跃迁可以绝对完美地描述电子激发,因此为了能充分描述这种情况的电子和空穴,笔者和合作者才创造了上述电子和空穴的具体定义,它把所有轨道跃迁全都纳入了考虑,可以理想、全面、充分地展现电子激发的特征。
很多人都知道NTO(自然跃迁轨道),笔者这两篇文章也有过专门的介绍:《使用Multiwfn做自然跃迁轨道(NTO)分析》(http://sobereva.com/377)、《跃迁密度分析方法-自然跃迁轨道(NTO)简介》(http://sobereva.com/91)。NTO通过对分子轨道进行酉变换,把分子轨道的跃迁转化为NTO的跃迁来描述,此时很多情况电子激发就可以只用一个占据的NTO向一个非占据的NTO之间的跃迁来较理想的描述了,此时空穴和电子可以分别当做这两个NTO的轨道波函数。NTO形式的空穴、电子和上述方式定义的空穴、电子各有利弊,NTO好处是保留了相位信息,这在讨论的时候有时候更便于判断空穴和电子对应什么类型轨道上,但是有很多情况,即便把电子激发变换成了NTO描述,还是没有哪一对NTO的跃迁起到绝对主导作用(比如最大的一对NTO跃迁只贡献80%),此时就必须用前面介绍的那种空穴、电子的定义,它对任何体系任何类型激发都是完美适用的。
2.2 空穴、电子分布的衍生量
基于上一节给出的Multiwfn中的空穴和电子的定义,可以定义几个有用的衍生量。首先我们可以定义激发态与基态的密度差:Δρ=ρele-ρhole。这在下文简写为CDD (charge density difference)。
注意激发态密度有非弛豫(unrelaxed)和弛豫(relaxed)两种。弛豫的激发态密度更为真实,与实际更为相符,但构造起来复杂耗时(需要利用Z-vector方法,耗时和算一次激发态受力相仿佛);而非弛豫密度构造比较简单,利用参考态轨道和组态系数就可以直接得到,可以认为是实际激发态密度的一阶近似,物理意义上可以理解为电子激发的一瞬间,电子结构还没来得及发生重排时的激发态密度。关于弛豫和非弛豫密度的更多信息见http://bbs.keinsci.com/thread-5738-1-1.html。之所以在这里提一下弛豫和非弛豫激发态密度的区别,是因为如上方式利用空穴和电子分布计算的CDD对应的是非弛豫的激发态密度与基态的密度差,而使用Multiwfn手册4.18.3节或《使用Multiwfn作电子密度差图》(http://sobereva.com/113)中的方式给出的是弛豫的激发态密度与基态的密度差,二者的差异从下图描述的一个体系的一种电子激发中可见一斑:
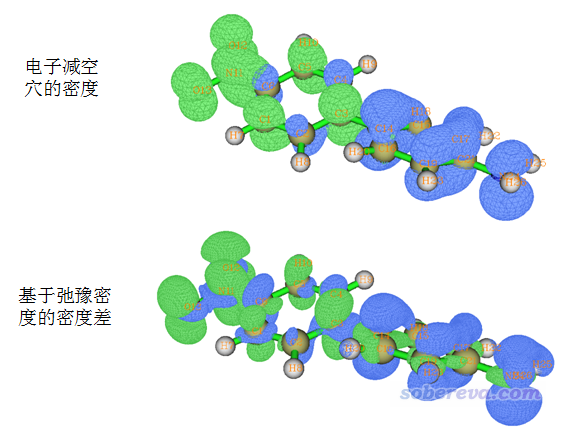
上面的CDD等值面图中,绿色是正值部分,对应激发态相对于基态电子密度增加的地方,蓝色是减小的地方。此图所示的激发是具有电荷转移特征的pi-pi*激发,因为从输出的组态信息上看只有pi轨道参与。图的上方是Multiwfn的空穴-电子分析给出的CDD,可见确实电子和空穴的等值面在共轭平面上都是有节面的,体现出纯粹的pi激发特征。然而下方的基于弛豫的激发态密度得到的CDD图上却同时体现了一丁点sigma电子特征,这是因为pi电子被激发后,由于电子间的相互作用势发生了改变,sigma轨道上的电子也出现了相应的响应。虽说基于非弛豫的激发态密度对应的CDD在原理上没有基于弛豫的激发态密度的那么严格,但是对于讨论电子激发特征是足够的(而且还避免了电子密度进一步弛豫对图像所产生的“干扰”)。平时我们会看到大量的计算文章中直接用MO或者NTO来讨论电子激发特征,实际上这种讨论方式相当于已经假定了激发态电子结构可以靠非弛豫密度充分地描述的这个前提了。
接下来,我们定义描述电子与空穴分布之间重叠的函数
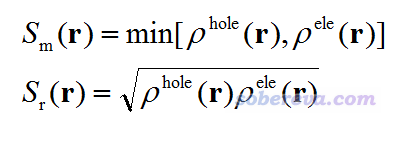
上面的Sm和Sr是描述重叠情况的两种不同的定义,前者是取空穴和电子的最小值,后者是取几何平均。两种定义没有绝对的优劣之分,都是合理的,容易证明Sr肯定大于Sm。我更倾向于用Sr这种定义,图像效果更好,数学意义也稍微强一些,因此后文我们都用Sr函数来讨论。通过绘制这两个函数,我们可以清楚地了解到哪些区域电子和空穴重叠比较显著。
2.3 分子轨道、原子、片段、基函数对空穴和电子的贡献
笔者将分子轨道对空穴和电子的贡献定义为以下形式,i和a是轨道标号。利用这样的数据可以立刻知道哪些分子轨道对跃迁起到重要作用,并且便于定量分析讨论
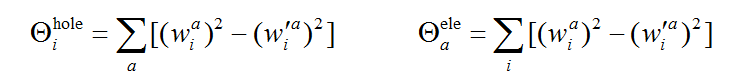
通过使用类似Mulliken方式的划分,可以按照下式计算原子和基函数对空穴和电子的贡献,A是原子标号,μ和ν是基函数标号,S是重叠矩阵,C是分子轨道展开系数矩阵
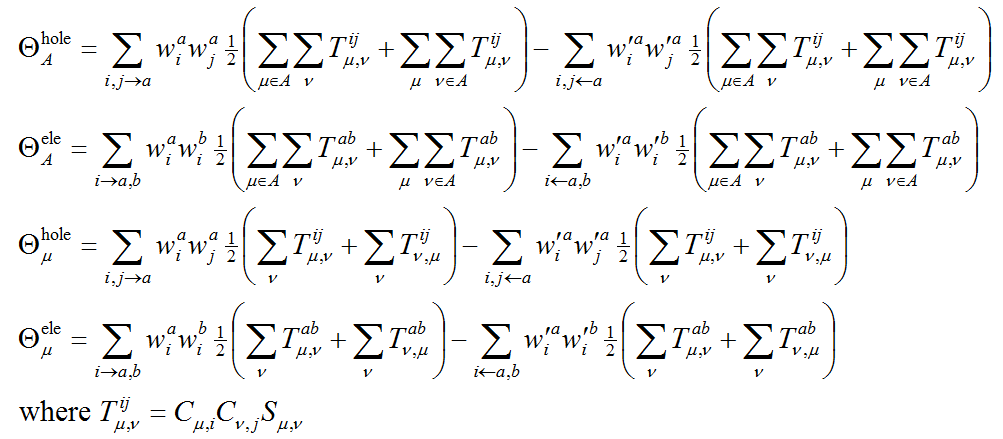
进一步,笔者定义了原子、片段对电子和空穴间差值(即CDD)的贡献,以及在原子、片段空间内电子与空穴的重叠量:
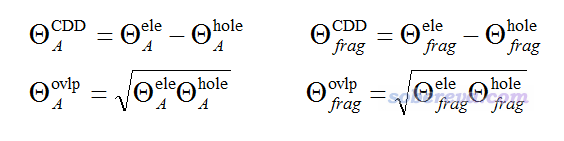
注意,以这种方式定义的原子/片段内的空穴与电子的重叠程度是不可加和的,比如在A原子和在B原子内重叠程度的加和不等于由A、B两个原子组成的片段内的重叠程度。类似地,还可以计算对应某基函数的空穴和片段的重叠量,以及基函数对空穴和电子间差值的贡献,就是把上面式子中原子标号改成基函数标号即可。
Multiwfn还直接支持通过Hirshfeld划分计算原子/片段对空穴和电子的贡献。
为了更便于考察,Multiwfn还支持把原子或片段对空穴、电子以及二者的重叠的贡献通过填色图形式展现,使得讨论起来更为直观,也便于在论文中把许多激发态的情况放到一起来对比,后面我们就会看到例子。
2.4 空穴和电子在全空间中分布特征的定量描述
为了便于通过一些定量数值衡量和讨论电子激发特征,笔者定义了Sm和Sr指数,即Sm和Sr函数在全空间进行积分:
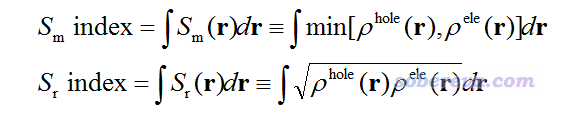
这两个指数越大,说明空穴和电子的重叠程度越高;数值越小,说明空穴和电子的分离越显著。Sr指数肯定大于Sm指数。这两个指数的值域都是[0,1],1就代表空穴和电子完美重合,0就代表没有丝毫交叠。
笔者还定义了衡量空穴和电子质心之间距离的D指数:
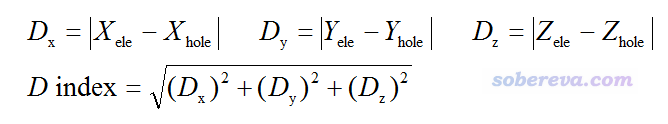
其中诸如X_hole指的是空穴的质心的X坐标,可以通过把ρhole函数乘上x坐标变量在全空间积分得到。所谓的质心就相当于函数整体分布的最中心、最具有代表性的那个点。
值得一提的是,激发态偶极矩相对于基态偶极矩的变化可以用空穴和电子质心的差值来直接计算。例如X分量的变化等于-(X_ele-X_hole),括号前头有个负号是因为电子带负电。
J. Chem. Theory Comput., 7, 2498 (2011)文章提出了基于密度差对电子激发特征进行分析的一系列指标,笔者发现这些指标也可以很好地挪用到空穴和电子特征的分析上(但很多指标的原始定义不理想或者缺乏普适性,我做了修改)。首先,对空穴和电子都可以定义σ,它的x,y,z三个分量相当于空穴或电子在x,y,z方向上分布的方均根偏差(RMSD),体现了分布广度或者说弥散程度。比如σ对于空穴的x分量定义为
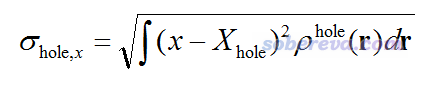
σ的模,即三个分量平方和开根号,笔者称之为σ指数,衡量的是空穴或电子的整体分布广度。
然后可以定义以下量
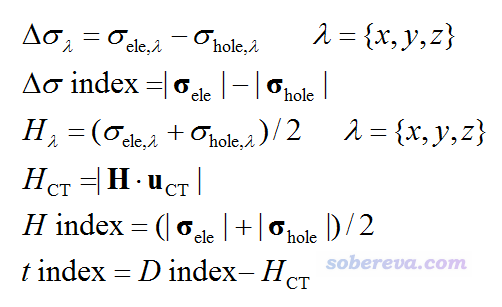
下面依次介绍下这些量的用途
Δσ_λ:衡量在λ方向上电子与空穴的空间分布广度之差。
Δσ指数:体现的是电子与空穴的总体空间分布广度之差。
H_λ:衡量在λ方向上空穴和电子的平均延展程度。
H_CT:衡量在CT方向上空穴和电子的平均延展程度。式中的粗体H就是H_x、H_y、H_z合在一起写成的矢量,粗体u_CT是CT方向上的单位矢量,利用电子和空穴的质心位置可直接得到。
H指数:体现的是电子与空穴的总体平均分布广度
t指数:衡量空穴和电子的分离程度。t指数>0就暗示由于CT使得空穴和电子分离较为充分,因为空穴和电子的质心距离较远,同时它们在此方向上的平均延展程度相对来说又不是那么高。t指数<0就可以认为在CT方向上空穴和电子没有显著分离,因为此时空穴和电子的质心距离相对于它们的平均延展程度来说没有那么大。
在《图解电子激发的分类》(http://sobereva.com/284)中介绍了怎么判断电子激发类型,常见的就是LE(局域激发)、CT(电荷转移激发),另外还有里德堡激发等。根据笔者的研究经验,利用上述指数,对电子激发类型一般可按照如下方式进行区分。
·局域激发(或整体激发):D指数小,Sr较大,t指数明显为负,Δσ指数不大。这种激发的空穴和电子主要分布范围很接近,重叠程度显然也低不了,空穴和电子分布没有明显分离,而且分布广度相仿佛
·单方向电荷转移激发:D指数大,其它指标大小不一定。既然是CT激发显然电子和空穴的距离必须大,而空穴和电子的重叠程度则可大可小,重叠大的时候说明电子和空穴分离尚不充分,而重叠小的时候说明电子和空穴分布已经高度分离了
·中心对称的电荷转移激发:有的体系电子激发时电荷转移可以往多个方向进行,中心对称的电荷转移激发是理想化的情况,应具有的特点是D指数小,Δσ指数很大
·里德堡激发:D和Sr指数都不大,Δσ指数很大。这种激发的空穴和质心距离相差一般不显著,但是电子分布范围远比空穴分布范围弥散,因此重叠度不会太高
以上判断方式对一般情况都是适用的,但也不排除遇到极个别反例的情况。可以在写论文的时候把一堆激发态的各种指数以列表方式给出来,但至少也应当同时考察一下空穴和电子分布图,这样在讨论时心里明显更有数、更放心,而不会被数字蒙在鼓里。
另外,别去苛求定义个诸如“D大于xxx就证明是电荷转移激发”这种判断标准,一刀切是使不得的。应该算作哪种激发,应当将各种指数还有空穴、电子分布图结合起来分析判断。另外,有的电子激发本身就是诸如CT和LE激发高度混合的模式,非要搞个严格标准来划分成要么CT要么LE一点意思也没有,也很有误导性。
笔者还定义了空穴离域指数(hole delocalization index, HDI)和电子离域指数(electron delocalization index, EDI),如下所示。HDI(EDI)数值越小,说明空穴(电子)离域程度越高,即分布的均匀程度越大、摊得越开。这两个量在定义上与笔者定义的轨道离域指数有类似之处,见《通过轨道离域指数(ODI)衡量轨道的空间离域程度》(http://sobereva.com/525)。
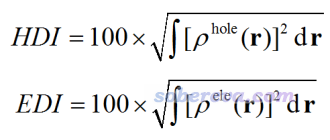
注:虽然|σ_hole|(|σ_ele|)越大往往也能暗示空穴(电子)的分布均匀程度越大,但对于空穴(电子)集中分布在多个区域的时候,就不能体现这点了,因为此指数假定空穴(电子)的主体分布能被单一高斯函数近似描述。而HDI、EDI则是普适的。
2.5 空穴、电子分布的平滑化描述
计算出前面提到空穴和电子的σ、质心位置后,根据J. Chem. Theory Comput., 7, 2498 (2011)的思路,笔者定义了可以把空穴和电子分布平滑化描述的Chole和Cele:
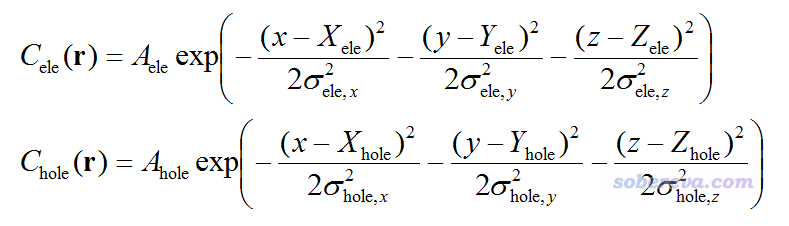
上式中A是归一化系数,使得Cele和Chole全空间积分都为1。x,y,z是坐标矢量r的三个笛卡尔分量。如果你观看Cele或Chole等值面图,它们的正中心位置就恰好是质心位置。
定义Chole和Cele的意义在于,空穴和电子的分布往往比较复杂,等值面图节面多,往往空穴和电子分布还相互交替,给图形化考察带来不便。而Chole和Cele等于把空穴和电子的分布等效地用高斯函数描述,抹去了分布细节,此时空穴和电子的等值面图变成了椭圆形状,在图形化考察时明显更为清楚、直观。如果Chole或Cele等值面看起来比较接近圆形,说明空穴或电子在各个方向分布的延展程度比较相近;如果等值面看起来是明显的椭圆,就说明在长轴方向上延展程度比其它方向上高得多;如果等值面图是个扁圆,则说明在最短轴方向上延展程度都比其它方向上低得多。
2.6 空穴-电子间的库仑吸引能(激子结合能)
电子是带负电的,而电子离开的地方,即空穴,相应地带正电,因此电子和空穴之间有库仑吸引能,也被叫做激子结合能(exciton binding energy),可根据简单库仑公式计算,如下所示
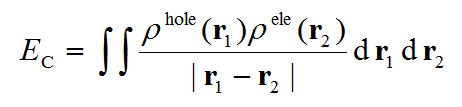
有不少文章通过上式计算并讨论了激子结合能,比如J. Chem. Phys., 143, 244905 (2015)、J. Phys. Chem. C, 121, 17088 (2017),但是他们是把本征值最大的占据和非占据NTO对应的密度作为上式中空穴和电子,显然没有Multiwfn里这种空穴和电子定义那么理想,因为很多情况下贡献最大的一对NTO跃迁对电子激发产生的贡献往往远到不了100%,偏差大到根本不可忽略,此时这样算的激子结合能也不准。
Multiwfn根据上式计算激子结合能的时候目前用的是基于均匀分布的格点方式算的,哪怕格点数不是特别多的时候耗时也还是很高的,建议用性能较好的服务器计算。而且耗时和格点数的二次方呈正比,而和格点间距六次方成反比。格点间距太大,则格点质量比较糙,虽然耗时低,但计算精度差;格点间距太小,精度好,但耗时会很高。因此格点间距应恰当选取,适当时候可以做计算结果随格点间距的收敛性测试,看什么时候结果基本不随格点数增加有明显变化,那么此时的格点数就够用了。
另外,激子结合能还有一种定义,就是垂直电离能(VIP)减去垂直电子亲和能(VEA)再减去optical gap(最低电子激发能)。这种定义和上面那种定义在理论上和实际数值上相差较大,没有显著联系。
2.7 Ghost-hunter指数
Ghost-hunter指数本身不属于空穴-电子分析范畴,但由于利用到前述的D指数,而且Multiwfn也会在空穴-电子分析过程中输出这个指数,所以这里顺带提一下。
纯泛函和低HF成份的杂化泛函对大共轭体系很可能出现ghost激发态,这是由于泛函的自相互作用误差(SIE)问题导致的虚假的电荷转移激发态。这些激发态的激发能很低,振子强度接近0,其存在会浪费计算量,还会妨碍正确判断、讨论感兴趣的激发态(比如初学者可能会把ghost态误当成了S1态去讨论荧光发射特征)。一般为了避免ghost态出现,可以用高HF成份泛函如M06-2X,或者长程校正泛函如wB97XD,或者长程区域HF成份很高的泛函如CAM-B3LYP来避免。为了判断当前TDDFT计算是否可能存在ghost态,J. Comput. Chem., 38, 2151 (2017)一文提出了ghost-hunter指数。笔者认为原文的定义不是特别理想和严格,而且存在错误,在Multiwfn的空穴-电子分析模块中计算ghost-hunter指数时用的是笔者自己在原始定义基础上稍作修改的定义:
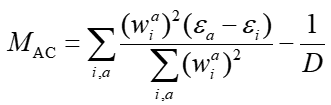
此式中,ε是分子轨道能量,i和a对应占据和非占据轨道,D就是前面提到过的空穴和电子质心之间的距离。ghost-hunter指数用M_AC符号表示,其对应的全称是Mulliken averaged configuration。JCC文章认为,ghost-hunter指数是电荷转移激发的激发能的理论下限,如果TDDFT算出来的某个态的激发能低于相应的ghost-hunter指数,这个态就算ghost态,反之就不算ghost态。这种判断方式有物理意义和合理性,但是根据笔者的实际测试发现,这种判断ghost态的标准往往太过激了。有时算出的激发能低于ghost-hunter指数一些,但凭基本理论知识可以判断出实际上这并不是ghost态。所以ghost-hunter指数仅供参考,顶多也就是当做判断ghost态的一个必要而非充分条件,千万别太盲目用它说事!如果你用的是诸如CAM-B3LYP或wB97XD这种长程区域HF成份较高或100%的泛函,其实根本不需要担心出现ghost态的问题,就算ghost-hunter指数判断成是ghost态也不要太当回事(尤其是激发能不是很低,且振子强度也不是特别接近0的情况,本来就不可能是ghost态)。
注意,JCC原文里计算ghost-hunter指数是基于昂贵的弛豫的激发态密度与基态密度差所计算出的D指数算的ghost-hunter指数,但在Multiwfn的空穴-电子分析模块里则是基于空穴和电子分布得到的D算的ghost-hunter指数,因此和原文的做法是存在定量差异的。Multiwfn中的这种实现是绝对合理的,可以放心使用。如果就是想基于弛豫的激发态密度与基态密度差对应的D来计算ghost-hunter指数,应该利用Multiwfn的基于密度差的电荷转移分析功能自行计算D,详见手册3.21.3节的介绍和4.18.3节的例子。另外注意,ghost-hunter指数只适合判断单方向的CT激发,不能用于判断多方向CT激发是否有ghost态的可能。
3 空穴-电子分析在Multiwfn中的使用简介
3.1 输入文件
Multiwfn主功能18中的子功能1用于实现空穴-电子分析(还能实现跃迁密度、跃迁偶极矩密度分析,本文暂不讨论)。此分析需要以下两类文件,更具体说明参见Multiwfn手册3.21节开头。
1 记录了参考态波函数的文件,是刚启动Multiwfn时就需要载入的
2 记录了激发态组态系数的文件,是进入空穴-电子分析功能时需要载入的
简单来说,对于Gaussian用户,要做空穴-电子分析一般就用TDDFT算激发态即可(不常用的CIS、TDHF、TDA-DFT也支持),闭壳层和开壳层参考态都支持,对单个结构做TDDFT以及对激发态用TDDFT做优化都可以(对于后者,分析的是最后一步结构的情况)。计算时候必须带IOp(9/40=4)关键词使得绝对值大于1E-4的组态系数都输出出来。把算完得到的chk转换为fch文件后就可以作为第1类文件,而Gaussian输出文件可作为第2类文件使用。
Multiwfn做空穴-电子分析最主要的一环就是计算空穴和电子的格点数据,从而能够可视化它们的分布,以及计算D、Sr/Sm、H、t等指数。对于较大体系,基于IOp(9/40=4)的输出文件计算空穴和电子的格点数据耗时往往还是挺高的,为了节约时间,可以改为使用IOp(9/40=3)关键词,这样输出的组态系数会少一些,显然空穴-电子分析的耗时就会降低不少,但代价是计算精度会有所损失,不过好在损失程度一般来说小到可以忽略。默认情况下Gaussian用的是IOp(9/40=1),此时空穴-电子分析误差就太大而根本无法接受了。
Multiwfn支持的一大堆电子激发分析,也包括此文介绍的空穴-电子分析,绝不仅限于Gaussian用户能用,诸如GAMESS-US、Firefly、ORCA等用户也可以用,详见手册3.21节开头的说明。很值得一提的是ORCA支持的sTDA和sTDDFT的任务的输出文件结合molden文件也可以用于当前分析。sTDA和sTDDFT分别是对TDA-DFT和TDDFT的高度简化,只要基态DFT轨道算出来了,则激发态就可以用这两种方法以近乎为0的耗时计算出来,因此Multiwfn的空穴-电子分析甚至可以用于超过500个原子的情况(因为DFT单点是可以算得动的)。
3.2 基本操作
进入空穴-电子分析功能后,会列出程序识别出的所有激发态的简要信息,并让你选择要考察的激发态。如果分析过之后还要分析其它态的话,先退出空穴-电子分析,然后再重新进入此功能并且选择其它激发态即可。在空穴-电子分析主界面里,有这些选项:
(1)计算空穴、电子、CDD、Sr、Sm、Chole、Cele以及跃迁密度、跃迁偶极矩等函数的格点数据。选这个选项后,先要对格点进行设定,相当于把体系套入一个矩形盒子里,盒子边缘与体系边缘原子有一定距离,要计算的格点均匀分布在这个盒子里。有了格点数据,才能进而可视化各种函数、通过格点积分方法计算各种指数。一般来说,小体系建议选中等质量格点(对应约512000个点),好几十原子的中等体系建议选高质量格点(对应约1728000个点);若是上百原子的大体系,1728000个点的情况下格点间距都可能偏大导致图像粗糙、各种指数计算不很准确,此时建议通过直接输入格点间距的模式设定恰当的格点间距(一般0.25~0.3 Bohr可以达到精度和耗时的权衡)。格点数据计算完了之后,前面提及的各种基于空穴和电子分布定义的定量指标以及其它一些指标如ghost-hunter指数都会输出出来。之后会看到后处理菜单,在里面可以观看各种函数的等值面图,也可以将它们导出成.cub文件便于之后在VMD等第三方程序里作图获得更好图像效果。后处理菜单还有相应的选项用于计算空穴和电子之间的库仑吸引能。
(2)输出分子轨道对空穴和电子的贡献。由于分子轨道数目太多,全输出的话太占屏幕,因此程序会让你输入个阈值,只有对空穴或电子贡献大于这个阈值的轨道才会被显示出来。
(3)输出原子或片段对空穴和电子的贡献并且绘制成填色图。进入此功能后,先选择计算原子对空穴、电子贡献的方法,然后屏幕上马上输出各个原子对空穴、电子以及Sr指数的贡献百分比。之后会出现个菜单,用相应选项可以把贡献值导出到文本文件里、把原子对空穴/电子/Sr指数的贡献绘制成热图(heat map,即填色矩阵图)、调节作图选项。若选择-1就可以定义片段,片段可以直接输入,也可以从你指定的文本文件中读取(此文件里每个片段定义占一行,内容比如1,5-10,12,19,可以有无数个片段),之后屏幕上马上就会输出各个片段对空穴、电子以及Sr指数的贡献百分比。然后再用相应选项绘制热图的时候,横坐标就不再是原子序号了,而是片段序号。
计算原子对空穴、电子贡献的方法可以选择Mulliken和Hirshfeld两种(见下文)。Mulliken方式计算的耗时极低,但是计算激发态时候用的基组绝对不能带弥散函数,否则结果将毫无意义。另外,由于Mulliken划分形式的理论缺陷,有的原子对空穴或电子的贡献有可能为负值,这种情况就把贡献视为0就完了,这样的原子的Sr指数会被Multiwfn自动当成0。但如果负值很明显,比如超过-3%,那么当前的结果就很不可靠了。如果由于特殊原因不得不用弥散函数(比如计算阴离子体系的激发态或者里德堡激发),或者用Mulliken方式计算原子对空穴和电子的贡献时出现特别显著的负值,那么建议选择Hirshfeld方式计算,这明显更昂贵,但是更可靠,非常普适。
顺带一提,Multiwfn还能基于Becke或Hirshfeld-I等方式计算原子或片段对空穴/电子的贡献,但需要手动操作,由于步骤略多且比起Hirshfeld划分没明显额外好处,故一般没必要用:先用空穴-电子分析模块的选项1计算空穴和电子的格点数据,然后把格点数据导出为cub文件。然后把settings.ini里的iuserfunc设为-1(此时用户自定义函数将对应于基于格点数据插值产生的函数),启动Multiwfn并载入电子或空穴的cub文件,进入主功能15(模糊空间分析),先利用选项-1选择要用的划分方式,然后选选项1(在各个原子模糊空间内积分特定函数),被积函数选择用户自定义函数,之后各个原子的贡献值就输出了。如果要计算某个片段贡献的话,在模糊空间分析模块中选择选项1之前先选选项-5来定义片段即可,之后子功能1计算出来的所有原子加和值就对应了你定义的片段的贡献量。
(4)输出基函数对空穴和电子的贡献。输入一个阈值后,对空穴或电子贡献超过这个阈值的基函数就会被输出。这对于考察哪些原子轨道显著参与了空穴和电子非常有用。只要搞清楚基函数与原子轨道间的对应关系,就可以通过把基函数对空穴/电子贡献数值加和得到原子轨道对空穴/电子的贡献。如果不知道对应关系怎么判断,参看《利用布居分析判断基函数与原子轨道的对应关系》(http://sobereva.com/418)。
Multiwfn里有很多选项,几乎都是光看屏幕上的提示就知道怎么用、是什么含义、该输入什么,这里就不具体说了,请睁大眼睛看清楚屏幕上的各种提示、仔细理解提示的含义,若还有不懂的请仔细阅读本文、手册相关章节并且自行尝试。
4 空穴-电子分析实例
下面将通过三个具有代表性的体系演示Multiwfn的空穴-电子模块的使用,一个是D-pi-A体系,一个是配合物体系,一个是里德堡激发的研究。如果对Gaussian的TDDFT计算不熟悉,务必参看《Gaussian中用TDDFT计算激发态和吸收、荧光、磷光光谱的方法》(http://sobereva.com/314)。本文例子的输入输出文件皆可在此下载:http://sobereva.com/attach/434/file.rar。本文使用的是Gaussian16 A.03版。
4.1 D-pi-A体系:NH2-biphenyl-NO2
首先我们对NH2-biphenyl-NO2体系的几个激发态用空穴-电子分析框架里的方法进行电子激发特征的讨论。此体系结构如下,NH2是电子给体(Donor)基团,联苯起到pi桥作用,NO2是电子受体(Acceptor)基团。
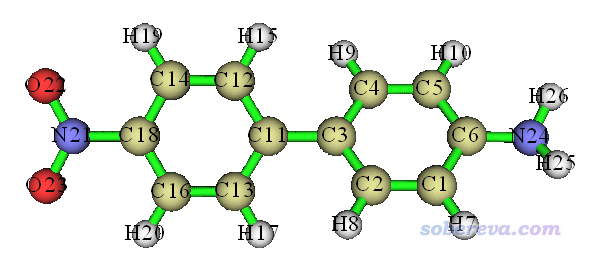
首先对此体系在常用的B3LYP/6-31G*级别下进行优化,然后用以下设定做TDDFT计算,将得到5个单重态激发态。IOp(9/40=4)如前所述必须要加上。
%chk=D-pi-A.chk
# CAM-B3LYP/6-31g(d) TD(nstates=5) IOp(9/40=4)
计算完毕后将D-pi-A.chk转换为D-pi-A.fch,不会转换的话看《详谈Multiwfn支持的输入文件类型、产生方法以及相互转换》(http://sobereva.com/379)。用CAM-B3LYP是因为此泛函做TDDFT描述电荷转移激发比较不错,当前体系有一些激发态是电荷转移激发态。普通有机体系用6-31G*做TDDFT就足矣得到合理的结果。
启动Multiwfn,依次输入
D-pi-A.fchk //首先载入含有参考态波函数信息的文件
18 //电子激发分析
1 //空穴-电子分析
D-pi-A.out //Gaussian输出文件,里面含有空穴-电子分析需要的组态系数信息
1 //首先我们分析基态(S0)到第1激发态(S1)的电子激发特征
1 //考察空穴、电子等函数的图形及各种指数
2 //当前体系不大,用中等质量格点就够了
此时屏幕上输出了大量信息,如下所示。凡是涉及到积分得到的指数,比如D、Sr等,都是通过均匀格点积分得到的,显然格点质量越高(间距越小),数值误差会越小。
Integral of hole: 1.000343
Integral of electron: 0.999793
Integral of transition density: -0.000033
Transition dipole moment in X/Y/Z: 0.444063 -0.000186 -0.001753 a.u.
Sm index (integral of Sm function): 0.27369 a.u.
Sr index (integral of Sr function): 0.51896 a.u.
Centroid of hole in X/Y/Z: -4.531729 0.000425 0.003252 Angstrom
Centroid of electron in X/Y/Z: -4.010033 0.001760 0.002643 Angstrom
D_x: 0.522 D_y: 0.001 D_z: 0.001 D index: 0.522 Angstrom
Variation of dipole moment with respect to ground state:
X: -0.985930 Y: -0.002523 Z: 0.001150 Norm: 0.985934 a.u.
RMSD of hole in X/Y/Z: 1.443 1.160 0.437 Norm: 1.902 Angstrom
RMSD of electron in X/Y/Z: 1.596 0.974 0.634 Norm: 1.974 Angstrom
Difference between RMSD of hole and electron (delta sigma):
X: 0.153 Y: -0.186 Z: 0.197 Overall: 0.072 Angstrom
H_x: 1.520 H_y: 1.067 H_z: 0.536 H_CT: 1.520 H index: 1.938 Angstrom
t index: -0.998 Angstrom
Hole delocalization index (HDI): 22.68
Electron delocalization index (EDI): 17.11
Ghost-hunter index: -18.831 eV, 1st term: 8.771 eV, 2nd term: 27.601 eV
Excitation energy of this state: 3.907 eV
Integral of hole和Integral of electron分别是空穴和电子在全空间的积分值,理论上应该恰好是1.0,但由于数值积分终究有误差,所以我们算出来的稍微偏离1.0,但由于偏离极小,因此对于当前体系当前的激发态来说,我们用的格点设定是合适的。如果发现偏离1.0非常大,那么得到的各种指数也都会不可靠,可能性有三:(1)忘了用IOp(9/40=3或4) (2)格点质量太低 (3)盒子的延展距离不够大,导致在空穴/电子有明显分布的区域没有被格点覆盖(尤其是考察里德堡激发时,默认的延展距离肯定不够大)。对后两种情况,在格点设定的界面里用相应选项进行调整即可。
上面输出的其余部分依次是:跃迁密度在全空间的积分(理想值为0)、跃迁电偶极矩、Sm和Sr指数、空穴和电子的质心坐标、Dλ和D指数、激发态偶极矩相对于基态偶极矩的变化的X/Y/Z分量和模、空穴和电子的RMSD、空穴和电子的RMSD在X/Y/Z方向的差值(Δσ_λ)以及Δσ指数、H_λ和H_CT和H指数、t指数、空穴和电子离域指数、Ghost-hunter指数、激发能。Ghost-hunter index后面的1st term和2nd term后面的两个值分别是Ghost-hunter指数表达式中的第一项(依赖组态系数和轨道能量的部分)和第二项(1/D),二者之差就是Ghost-hunter index。最后给出的激发能是从Gaussian输出文件里直接读的。
上面输出的跃迁偶极矩是利用均匀格点积分得到的,从Gaussian输出文件里也可以直接读到,X/Y/Z三个分量为0.4427、-0.0005、-0.0012 a.u.,这和Multiwfn输出的0.444063、-0.000186、-0.001753 a.u.极为相近,这也进一步表明当前的积分格点设置是合理的。
当前S0->S1这个激发,从上面的输出中看到D指数才0.522埃,还不到半个C-C键的长度,明显算是个很小的值。而Sr指数达到0.519(上限值为1.0),相当于空穴和电子有一半多一点的分布特征都已经完美重合上,故已经算很大了。所以,光从Sr和D,我们就已经能判断这应该是一个LE激发。我们再看t指数,总值为-0.998,明显小于0,这意味着空穴和电子的分布没有显著的分离,同样也暗示了这应该是个LE激发。
现在屏幕上会看到后处理菜单,每个选项的含义都不言自明,请读者仔细浏览一遍每个选项。这里我们选择3,会同时看到空穴和电子的分布,如下图的上半部分所示。然后关闭图形窗口,选择8来同时观看Chole和Cele,如下图的下半部分所示,为了看着清楚用了透明风格(图形窗口上方有菜单可以设置显示风格)。图中绿色代表电子分布,蓝色代表空穴分布。绘制的时候等值面数值(isovalue)都是设的0.005,设多大合适没有确切标准,应该反复调节,看什么时候对应的等值面图最能把当前电子激发的主体特征充分展现出来并且便于我们讨论(提醒:对于Chole和Cele分布得极其广阔的情况,它们的等值面在默认的isovalue下是看不到的,必须自己逐渐一点点减小isovalue直到能看得到为止)。
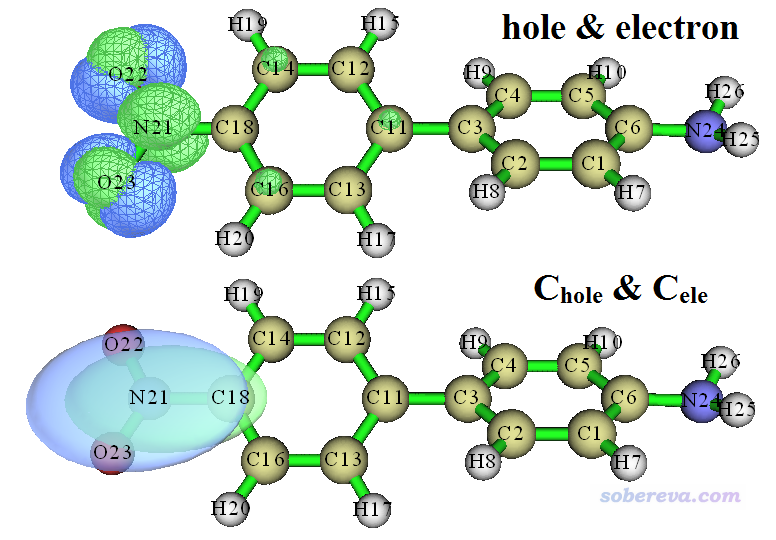
由上图可见,空穴和电子几乎只出现在硝基部分,因此毫无疑问S0->S1是局域激发,验证了我们基于D、Sr、t指数所下的结论。Chole和Cele的图形看上去显然更直观一些,非常圆滑,没有空穴和电子分布图那么多节面。另外,根据上面的空穴图,空穴看起来是由氧的孤对电子轨道构成的,因为在每个氧两侧各有一个瓣,而且没用于成键;而从电子图上看,电子在NO2的平面上有个节面,因此电子分布应当是由pi*轨道构成的,故我们可以将S0->S1指认为n->pi*特征的局域激发。
我们接下来看一下空穴和电子的重叠函数。在当前的图形窗口上点Return,在后处理菜单选选项4,然后选2,就显示出了Sr函数图,如下图上半部分所示。关闭窗口,选择7,就显示出了激发态与基态间的密度差(CDD)图,如下图下半部分所示,绿色和蓝色分别对应激发态密度相对于基态密度增加和减少的部分。绘制这两个图的时候用的等值面数值都是0.005。
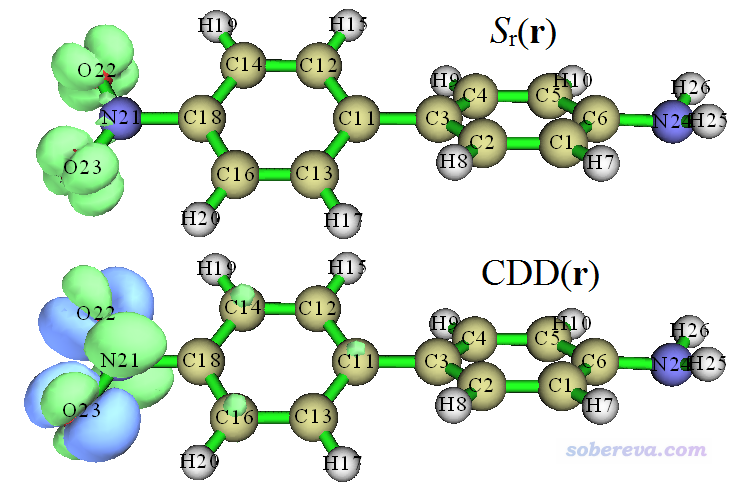
从Sr图上,可以清楚看出空穴和电子在哪些地方有显著交叠。如上图所示,每个氧周围有四个空穴与电子高度交叠的区域,对照之前的空穴和电子等值面图就很容易明白Sr图形为什么是这样。上面的CDD图和之前展示的把空穴与电子同时显示在一起的图(简称为“空穴&电子图”)比较像,但是也存在差异,关键差异就在于CDD把电子和空穴求差,展现的是二者在交叠区域已经发生过抵消的图;而空穴&电子图当中则是可以看到空穴与电子之间的相互交叠特征的。我认为空穴&电子图比CDD明显更适合考察电子激发的内在特点,因为它直接展现出了未经抵消过的空穴和电子的原始分布特征。
我们若在后处理菜单中选择18,程序就会开始计算空穴-电子之间的库仑吸引能,计算较为耗时,输出为:
Coulomb attractive energy: 0.287031 a.u. ( 7.810524 eV )
接下来,再演示一下计算轨道对空穴和电子的贡献。在后处理菜单选择0,就退回到了电子-空穴分析界面,然后选择2,再输入一个输出阈值,这里输入1,代表把对空穴或者电子贡献超过1%的轨道输出。此时屏幕上马上看到以下内容:
MO 52, Occ: 2.00000 Hole: 96.207 % Electron: 0.000 %
MO 56, Occ: 2.00000 Hole: 3.415 % Electron: 0.000 %
MO 57, Occ: 0.00000 Hole: 0.000 % Electron: 85.411 %
MO 59, Occ: 0.00000 Hole: 0.000 % Electron: 12.222 %
MO 61, Occ: 0.00000 Hole: 0.000 % Electron: 2.163 %
Sum of hole: 100.001 % Sum of electron: 100.001 %
由数据可见,MO52对空穴产生绝对主导,贡献达到96.2%,而电子则主要由MO57构成,贡献达到85.4%。这说明,如果你只通过MO52和MO57这两个轨道来说事,虽然能对这个电子激发予以定性的描述,但还是有不可忽略的偏差。上面Sum of hole和Sum of electron分别是所有轨道对空穴和电子的贡献的总和(包括屏幕上没有输出的项),显然理应为精确的100%,但可见当前输出值有个0.001%的误差,完全可以忽略,这误差来自于Gaussian输出文件里并没有输出所有的组态,我们通过IOp(9/40=4)只要求了组态系数绝对值大于0.0001的才被输出。
我们再看看原子和片段对空穴和电子的贡献。在电子-空穴分析界面里选择3,然后选择1用Mulliken划分方式,之后马上看到以下输出:
The number of non-hydrogen atoms: 16
Contribution of each non-hydrogen atom to hole and electron:
1(C ) Hole: 0.19 % Electron: 0.02 % Overlap: 0.07 % Diff.: -0.17 %
2(C ) Hole: 0.18 % Electron: 0.48 % Overlap: 0.30 % Diff.: 0.30 %
3(C ) Hole: 0.59 % Electron: 0.13 % Overlap: 0.28 % Diff.: -0.46 %
4(C ) Hole: 0.18 % Electron: 0.49 % Overlap: 0.30 % Diff.: 0.32 %
5(C ) Hole: 0.19 % Electron: 0.02 % Overlap: 0.06 % Diff.: -0.18 %
6(C ) Hole: 0.31 % Electron: 0.37 % Overlap: 0.34 % Diff.: 0.06 %
11(C ) Hole: 0.15 % Electron: 4.17 % Overlap: 0.78 % Diff.: 4.03 %
12(C ) Hole: 0.41 % Electron: 0.14 % Overlap: 0.24 % Diff.: -0.26 %
13(C ) Hole: 0.37 % Electron: 0.14 % Overlap: 0.23 % Diff.: -0.23 %
14(C ) Hole: 0.94 % Electron: 5.03 % Overlap: 2.18 % Diff.: 4.09 %
16(C ) Hole: 0.92 % Electron: 5.01 % Overlap: 2.15 % Diff.: 4.09 %
18(C ) Hole: -0.01 % Electron: 1.16 % Overlap: 0.00 % Diff.: 1.17 %
21(N ) Hole: 2.39 % Electron: 33.90 % Overlap: 9.00 % Diff.: 31.52 %
22(O ) Hole: 46.18 % Electron: 24.38 % Overlap: 33.55 % Diff.: -21.80 %
23(O ) Hole: 46.12 % Electron: 24.39 % Overlap: 33.54 % Diff.: -21.73 %
24(N ) Hole: 0.46 % Electron: 0.15 % Overlap: 0.26 % Diff.: -0.32 %
由于氢原子一般不怎么参与电子激发,所以上面只输出了非氢原子的信息,包括原子对空穴、电子、空穴与电子的重叠、电子与空穴的差值(即CDD)的贡献,公式在本文2.3节已经介绍了。硝基上的原子序号是21、22、23,由数据可见,硝基的氧对空穴起了主导贡献,两个氧加起来贡献了92%。而电子分布的离域特征相对更强一些,硝基上的三个原子一共贡献了大约83%,剩下的大多是联苯上的原子贡献的。虽然通过考察空穴、电子等值面图就可以考察它们的分布特征,但是图像明显依赖于等值面选取,没法仅通过一张图就全面展现所有区域的空穴和电子分布特征。而如上给出的原子的定量贡献值,则是较确切、严格的。21N、22O和23O的Diff.加和约为-12%,体现出在硝基区域密度差的积分值是负值,即硝基部分是失电子的,有一部分转移到了联苯上(如果想考察具体转移量,建议用Multiwfn中的IFCT方法,见http://sobereva.com/433)。
我们还可以把原子的贡献值绘制成热图。在当前菜单里先选择4然后输入1,把横坐标步长间隔改为1,然后选择1 Plot hole/electron composition as heat map,就会马上看到以下图像

图中横坐标是非氢原子序号,从1开始连续排,此图通过颜色描述了各个非氢原子对空穴、电子以及二者重叠的贡献大小(诸如0.4就代表40%)。根据前面给出的非氢原子对空穴/电子的贡献数值列表,我们可以知道诸如图中横坐标为16的位置对应的实际上是N24原子。为了令图的横坐标和原子位置对应起来更方便,大家可以把fch/gjf/out文件用gview打开,进入Edit - Atom List,选Edit - Reorder - All atoms: Hydrogens Last,此时gview显示的就是以下图像,所有氢原子的序号都被放到非氢原子后头了,因此图中非氢原子的序号就和Multiwfn绘制的原子对空穴/电子贡献的热图的横坐标直接对应了。

和gview显示的序号一对照就知道,热图横坐标的13、14、15的位置对应硝基的氮和两个氧原子,16对应氨基的氮,其余的都是联苯上的碳。热图的hole那一行非常直观地体现出,空穴几乎完全是硝基的氧贡献的,因此相应矩阵元是红色,对应很大数值。电子主要也是由硝基贡献,但其它区域也有不可忽视的贡献,因此热图的electron那一行在13~15以外一些区域呈现了蓝色。热图的overlap那一行的颜色传达的信息是电子和空穴在硝基氧上有显著重叠(这和Sr函数等值面图看到的现象一致),而在体系其它区域的重叠则远没有这么显著。
在空穴/电子的成分分析界面里还有很多选项,可以调节热图的作图效果、把图像保存成图片文件、切换是否把氢原子也纳入热图,还可以把数据导出成he_atm.txt,以便之后自行在Origin等程序里绘制。这些选项就不一一说明了,请自行尝试。其中有个选项-1很重要,通过它可以载入片段定义,从而输出片段对空穴和电子的贡献,之后还能绘制基于片段的热图,这使得讨论明显更为方便。此处我们把体系按照以下示意的方式划分为四个片段
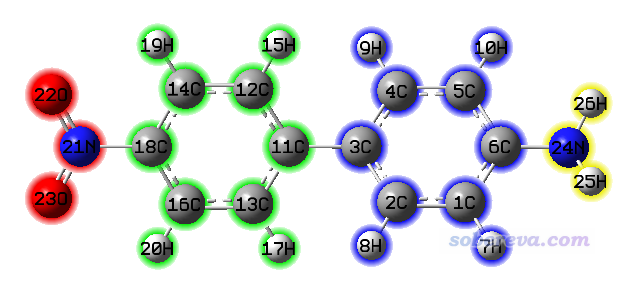
选择选项-1,然后依次输入
4 //定义四个片段(如果此处输入0,将从指定的文本文件里读取片段定义)
21-23 //片段1(硝基)的原子序号
11-20 //片段2(挨着硝基的苯)的原子序号
1-10 //片段3(挨着氨基的苯)的原子序号
24-26 //片段4(氨基)的原子序号
马上看到了如下输出
Contribution of each fragment to hole and electron:
# 1 Hole: 94.68 % Electron: 82.67 % Overlap: 88.47 % Diff.: -12.01 %
# 2 Hole: 3.20 % Electron: 15.67 % Overlap: 7.09 % Diff.: 12.47 %
# 3 Hole: 1.64 % Electron: 1.53 % Overlap: 1.59 % Diff.: -0.12 %
# 4 Hole: 0.47 % Electron: 0.13 % Overlap: 0.25 % Diff.: -0.34 %
基于片段给出的贡献数据比基于原子给出的贡献数据明显清晰、易于讨论得多。数据体现空穴有94.68%都在硝基上,而电子有82.67%在硝基上,其次有15.67%在挨着硝基的苯环上。在硝基上空穴与电子重叠有88.47%的程度。由于硝基上Diff.为-12.01%,当前考察的又是单电子激发,因此可以说硝基上的电子在电子激发过程中减少了0.1201个,这部分电子基本都跑到挨着硝基的苯环上了,由数据可见这个区域增加了0.1247个电子。然后,若想把上述数值展现得更直观,我们可以选选项1绘制热图,此时的横坐标已对应于片段编号了,如下所示:
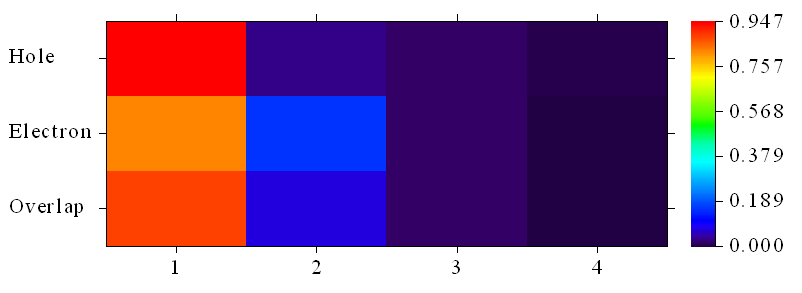
由图明显可见电子的分布广度大于空穴的。
到此,对NH2-biphenyl-NO2这个体系的S0->S1激发的空穴-电子框架中的各种分析已经完整做了一遍。如果想再分析其它激发态,通过选项0退回到主功能18的菜单中,再次进入空穴-电子分析功能,然后选择相应激发态即可。这里我们把这个体系所有算出来的5个激发态的D、Sr、H、t指数以及空穴-电子库仑吸引能放在一起对照。之前还没讨论过的空穴离域指数(HDI)和电子离域指数(EDI)也一并给出了:

下面是所有这些激发的空穴&电子图、Chole&Cele图,以及Sr函数图,绘制时候等值面数值用的都是0.003。可以看到Chole&Cele图总是可以把空穴&电子图蕴含的主体特征以更清晰直观的方式展现出来,尽管丢失了很多细节,因此没法判断电子激发具体类型,比如是n->pi*还是pi-pi*等等。
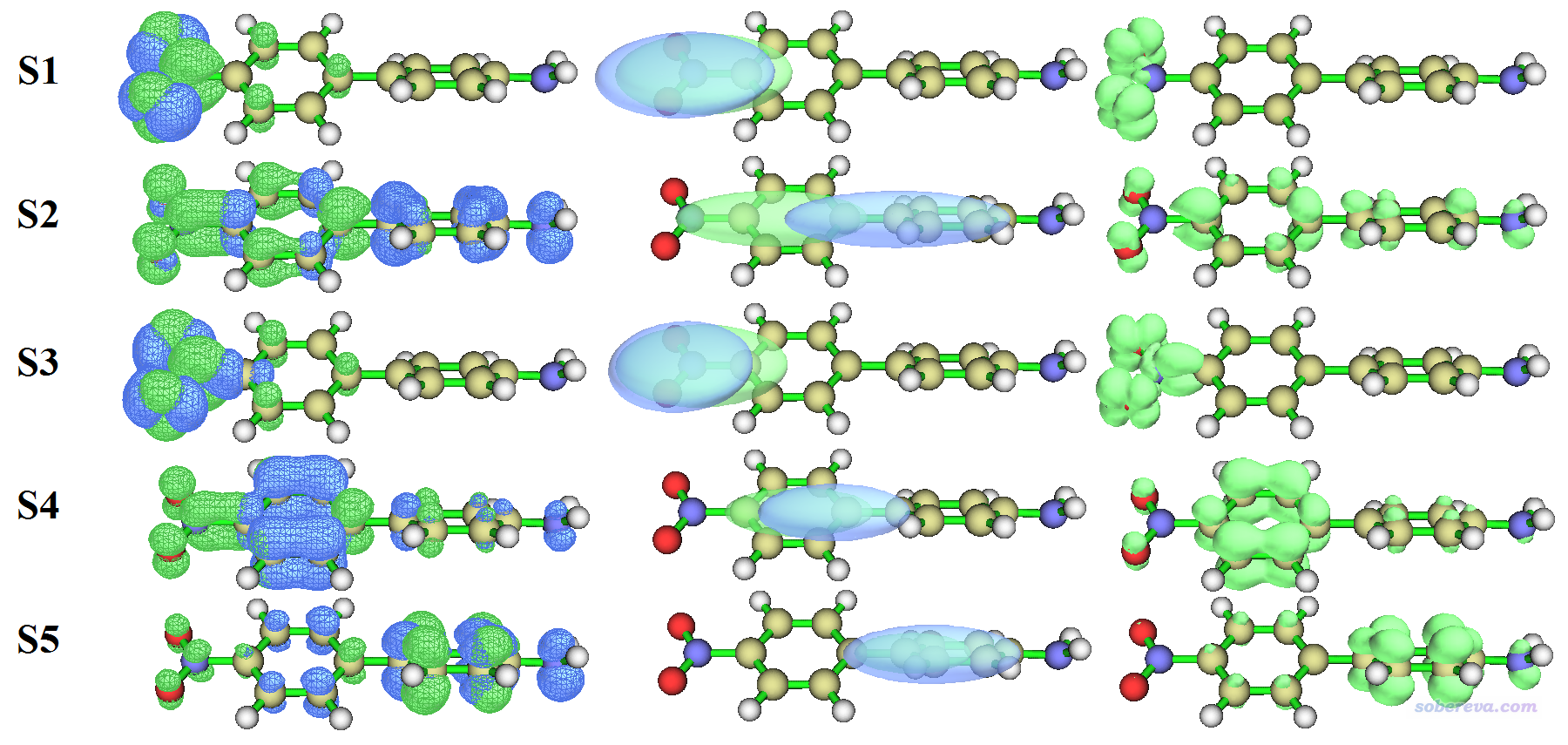
我们将指数和图形结合来看,首先看电荷转移距离。从D指数来看,只有S0->S2数值很大,高达3.48埃,明显可以认为是电荷转移激发,确实从Chole&Cele图上也看到蓝色和绿色等值面的中心(分别对应空穴和电子的质心位置)离得比较远,而其它电子激发的蓝色和绿色等值面中心相距都很近,明显只能算是局域激发。
再看Sr指数,我们看到所有激发态的Sr指数都比较大,特别是S0->S4和S0->S5特别大,高达0.87,结合Sr函数图和空穴&电子图我们可以知道原因在于这两种激发都是苯环上的高度局域的pi-pi*激发。虽然S0->S1也是高度局域的激发,但是它的Sr(0.52)甚至比S0->S2那种CT激发的Sr(0.65)还小,这是因为前面说过S0->S1体现的是n->pi*特征,由于孤对电子分布主体在NO2平面上,而pi*在NO2平面上是节面,因此S0->S1的Sr不算特别大,但也绝对算不上小。
再看H指数,反映了空穴和电子的平均分布广度。从空穴&电子图上可以看出,S0->S1和S0->S3激发的空穴和电子主体都分布在NO2那一小块地方,因此H指数不大;而S0到S2、S4、S5的激发对应的空穴和电子的分布范围都比较广(在0.003等值面下,等值面甚至在整个体系各处都能看得到),因此H指数相对较大。从t指数上看,只有S0->S2的t指数为轻微的正值,表明空穴和电子分离较为明显,因此更有理由把S0->S2认为是CT激发。而S0向其它激发态的激发对应的t都为显著的负值,暗示电子与空穴分离度很低。
结合以上图形和数据,我们可以对基态到5个激发态的特征进行确切的指认:
S0->S1:硝基上n-pi*局域激发
S0->S2:氨基到硝基方向上的pi-pi*电荷转移激发
S0->S3:同S0->S1
S0->S4:发生在与硝基相连的苯环上的pi-pi*局域激发
S0->S5:发生在与氨基相连的苯环上的pi-pi*局域激发
上面给出的空穴-电子库仑吸引能和电子激发特征有密切关联,对其影响最大的是D。容易理解,D越大,空穴和电子主体分布越远,因此空穴和电子的库仑相互作用应当更弱。从数据看,确实S0->S2这个唯一的CT激发的空穴-电子库仑吸引能的大小是所有5个电子激发中最小的,为4.71 eV。而S0->S1和S0->S3的激发,一方面D非常小,另一方面从H指数上看其空穴和电子分布的空间范围又非常窄,可想而知憋在这一小块地方的空穴和电子之间的库仑吸引会非常强,从前面的表中来看确实如此,它们的空穴-电子库仑吸引能是最大的(7.81和8.54 eV)。
将HDI、EDI分别与空穴、电子等值面进行对比,我们可以看到这两个指数确实能很好地区分不同激发态的空穴和电子的空间离域程度的高低。比如对于S0->S1和S0->S3激发,从等值面图上可见,它们的空穴和电子分布都是高度局域在硝基部分的,因此HDI和EDI都是相对较大的数值。而S0到其它三个激发态的跃迁的HDI和EDI都小得多,表明它们的空穴和电子都有明显的离域特征,确实从等值面图上也能看出这一点。因此HDI、EDI在定量化讨论空穴和电子分布的离域程度方面很有价值、很靠谱。
这里也把所有5个激发态对应的片段对空穴、电子和二者重叠的贡献的热图合在一起给出。是在Multiwfn输出的五个激发态的图像的基础上稍微做了些拼接。图中左上角示意了对片段的划分。为了便于横向对比,所有激发态的这个图的色彩刻度统一设为了0.0~1.0。
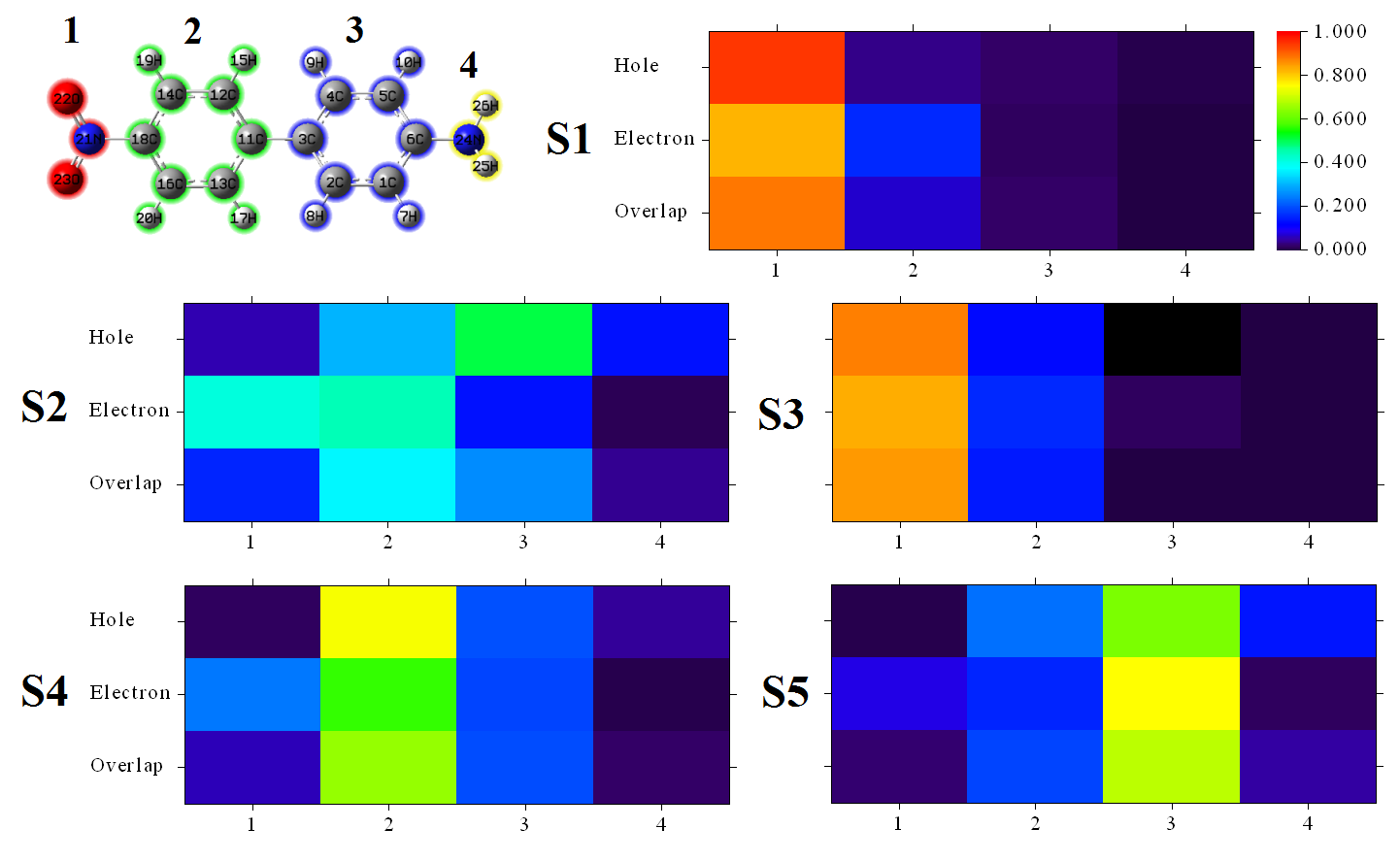
从这个图上,看一下空穴和电子对应的行上的色彩鲜明的区域,就马上知道电子是从哪转移到哪的,比如从S0->S2的图一看就知道被激发的电子主要来自片段3(靠近氨基的苯),大部分转移到了片段1(硝基),少部分转移到了片段2(靠近硝基的苯);其空穴和电子重叠区域比较分散,在片段2处重叠程度相对而言最高。再比如从S0->S4的图上可看出被激发的电子是片段2的,激发后大部分还是留在片段2,但是也有一部分跑到了片段1,而空穴和电子的重叠在片段2上显著高于其它部分。
这个NH2-biphenyl-NO2体系在《在Multiwfn中通过IFCT方法计算电子激发过程中任意片段间的电子转移量》(http://sobereva.com/433)中也做了分析,文中将IFCT方法和空穴-电子分析相结合,在定量层面上透彻考察了电子激发过程中片段间电子转移量,这是很有价值的信息,此文大家务必要看。
在空穴-电子分析的后处理菜单有很多选项可以把各种函数导出成cube文件,之后可以在免费的VMD程序(http://www.ks.uiuc.edu/Research/vmd/)里绘图以获得更好效果,笔者录了一段视频以演示具体操作,请大家观看:《使用Multiwfn和VMD对配合物激发态绘制空穴-电子等值面图》(https://www.bilibili.com/video/av28242597)。明显更为理想的做法是利用笔者写的VMD脚本来将空穴和电子绘制到一起,见《在VMD里将cube文件瞬间绘制成效果极佳的等值面图的方法》(http://sobereva.com/483),操作简单至极,比手动在VMD里点击各个选项来操作简单得多,而且图像效果极佳,如下所示(对应本例的S0-S4跃迁):
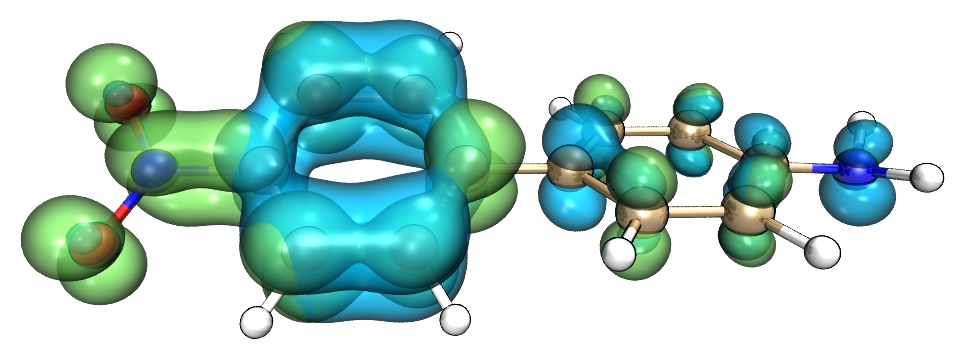
下图是笔者在《一篇最全面、系统的研究新颖独特的18碳环的理论文章》(http://sobereva.com/524)对电子结构非常特殊的18碳环体系的S0->S1的激发用Multiwfn+VMD得到的空穴-电子等值面图,可见非常漂亮,在此文中利用了这种分析对18碳环的电子激发特征做了透彻的分析,十分建议一读!

另外,还可以在VMD里面利用绘图命令在Chole&Cele的图像上把质心位置标出来,使图像上的信息更丰富。具体来说就是先在VMD里按如上方法把Chole&Cele的等值面图绘制出来后,在VMD窗口中输入类似以下命令
draw color purple
draw sphere {1.411500 -0.007015 -0.025494} radius 0.25 resolution 20
draw color orange
draw sphere {-2.069784 -0.000346 -0.000830} radius 0.25 resolution 20
这里draw color代表设定接下来绘制的物体的颜色,draw sphere用来在指定位置绘制半径为radius的圆球。对于当前体系的S0->S2激发,对应的Chole&Cele的等值面如下,紫色和橙色圆球分别是空穴和电子的质心。为了更便于它人理解,还自行画了个箭头上去表示电子转移方向,同时标注上了D指数。
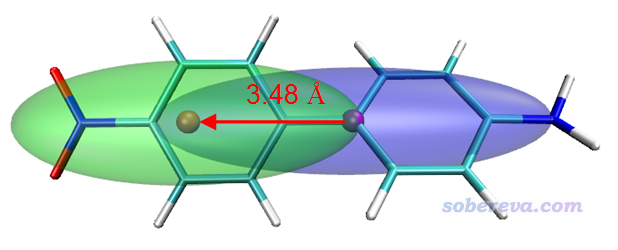
4.2 配合物体系:Ru(bpy3)2+阳离子在水环境中
下面我们通过空穴-电子分析考察一下下面这个Ru(bpy3)2+阳离子配合物在水中的几个激发态。
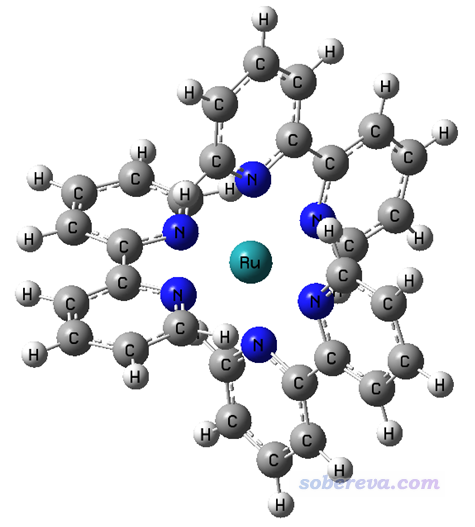
相应的Gaussian输入文件在本文的文件包里,从中可见关键词是
B3LYP/genecp TD(nstates=50) scrf IOp(9/40=3)
这里写scrf就代表用Gaussian16默认的IEFPCM隐式溶剂描述水环境。由于此体系比较大,而且一次算50个激发态,为了避免计算空穴-电子分析耗时太高,以及避免输出文件太大,这里用的是IOp(9/40=3),实际上此时的空穴-电子分析精度已经完全够了。此例对配体用的6-311G*,对Ru用的SDD赝势基组。
我们随便选取几个激发态使用Multiwfn做空穴-电子分析,结果如下

表中的D指数都非常小,而Sr指数都很大,这主要是因为当前体系是个对称体系。表中的MLCT(%)是指metal-ligand charge transfer(金属向配体电荷转移)百分比。之前在《电子激发过程中片段间电荷转移百分比的计算》(http://sobereva.com/398)里专门讨论过怎么算,实际上利用空穴-电子分析的数据也可以算,而且很理想,就是将金属在空穴中的百分比(即hole(Ru%))减去金属在电子中的百分比(ele(Ru%))。注意,确切来说,这种方式得到的是净MLCT量,里面已经和LMCT量(配体向金属电荷转移量)做了一定抵消。
下面是相应的空穴&电子图,等值面数值都是0.002。由于S0->S24跃迁的空穴和电子分布区域有很大重叠,导致电子在金属部分被空穴的等值面遮盖,为了看得清楚,这里把空穴和电子的等值面单独给出(在空穴-电子分析后处理菜单里有选项单独显示二者。单独显示空穴的时候等值面是绿色的,如果你把等值面数值改为负值,等值面就变成了蓝色了)

将图形和定量数据结合可以很明显看出,S0->S24激发既有metal-centered (MC)特征,即金属上的电子激发到金属自己的空轨道上,同时也有很高的MLCT成份。正如空穴&电子等值面图所示,空穴的等值面主体是在金属上,而电子的等值面则能看出有很大一部分跑到配体上去了。我们算出来的MLCT特征百分比为77.3-19.6=57.7%,应当说和空穴-电子等值面图传达的信息非常相符。注:空穴在配体上其实也有不可忽视的分布量,为100%-77.3%=22.7%,之所以空穴图上没看到,是因为空穴的分布在配体上摊得非常开,密度处处都不大,因此只有把等值面数值设得更小,比如0.0005,才能清楚看到空穴在配体上的分布。
再看S0->S37,从等值面图可见空穴和电子的主体都在一个配体上,因此毫无疑问这是个LC (ligand-centered)激发,是这个配体的pi电子激发到它自己的pi*轨道上。由于空穴在金属上也能看到一些分布,因此也有点MLCT特征,算出来是8.1%。
最后再看S0->S40,从空穴图形和表格里的空穴在金属上的百分比上看,空穴的分布特征和S0->S24别无二致,但电子在配体上的分布量明显没有S0->S24那么大,也就是有一定分布在和Ru直接配位的四个氮上,因此S0->S40的MLCT特征明显弱于S0->S24,而相反,它的MC特征肯定比S0->S24的要大得多。
顺带一提,对这种配合物体系,你若想把MLCT、LMCT、LLCT、MC、LC特征具体数值全都分别得到的话应当用Multiwfn的IFCT分析,见《在Multiwfn中通过IFCT方法计算电子激发过程中任意片段间的电子转移量》(http://sobereva.com/433)。
我们已经知道,S0激发到S24和S40的过程中电子主要来自Ru原子,但如何判断被激发的是Ru的哪个原子轨道的电子?虽然从空穴的等值面图上也多多少少能判断出来,但还是有一些主观性。为了弄清楚这点,我们可以计算基函数对空穴和电子的贡献。例如进入空穴-电子分析功能后选择第40个激发态后,我们选4 Show basis function contribution to hole and electron,然后输入一个输出阈值,比如输入2,此时屏幕上就出现了对空穴或电子贡献超过2%的各个基函数信息:
Basis Type Atom Shell Hole Electron Overlap Diff.
22 D 0 1(Ru) 12 23.81 % 0.00 % 0.33 % -23.81 %
23 D+1 1(Ru) 12 8.90 % 13.63 % 11.01 % 4.72 %
24 D-1 1(Ru) 12 9.06 % 25.12 % 15.09 % 16.05 %
25 D+2 1(Ru) 12 13.96 % 6.94 % 9.84 % -7.02 %
26 D-2 1(Ru) 12 14.06 % 15.57 % 14.80 % 1.51 %
27 D 0 1(Ru) 13 3.66 % 0.00 % 0.06 % -3.66 %
30 D+2 1(Ru) 13 2.32 % -0.01 % 0.00 % -2.32 %
31 D-2 1(Ru) 13 2.33 % -0.03 % 0.00 % -2.35 %
Sum of above printed terms: 78.10 % 61.22 % 16.88 %
由数据可见,对空穴产生主要贡献的都是Ru的D基函数,我们当前用的SDD赝势基组对Ru只描述了它的4s,4p,4d,5s电子,因此S0->S40跃迁时被激发的电子绝大部分都是Ru的4d轨道上的电子。在Ru原子上,对电子有贡献的也都是D基函数,因此S0->S40中的MC成份对应的是Ru上面的d-d激发,这是由于Ru与配体配位后,d轨道能级发生分裂,因此出现了占据的d轨道的电子被激发到了非占据的d轨道的现象。(判断被激发的电子所属轨道其实也不是只有上述这一种做法,比如也可以用Multiwfn做NTO分析,然后用Multiwfn的轨道成份分析功能去考察本征值最大的那个占据的NTO的成份或者直接观察NTO图形。但如前所述,如果当前研究的电子激发没法很好地通过一对NTO描述,这种做法就不灵了,而空穴-电子分析则没有任何局限性)。
4.3 里德堡激发例子:甲醛
里德堡激发就是电子从价层占据轨道激发到弥散程度非常高的里德堡轨道的情况,在《图解电子激发的分类》(http://sobereva.com/284)中已经介绍过。这里以甲醛为例,示例一下通过空穴-电子分析考察里德堡激发的情况。计算里德堡激发的基组必须带有充分的弥散函数,而且应该用较高HF成份,至少是长程区域有较高HF成份的泛函,所以此例用的关键词为CAM-B3LYP/aug-cc-pVTZ IOp(9/40=4) TD(nstates=10)。相应的Gaussian输入输出文件都在本文的文件包里。
我们按照前述过程,照常做电子-空穴分析。注意,设定格点的那一步,必须选择-10 Set extension distance of grid range for mode 1~4来修改格点数据边界相对于分子边缘原子的延展距离,然后输入一个较大的值,比如10 Bohr。因为目前版本默认的延展距离对于里德堡激发的分析来说太小,会导致里德堡轨道十分弥散的特征有很大一部分会被截断。
当前总共算了10个激发态,下图中把其中一些有代表性的激发态的分析结果列了出来。前四个图都是空穴&电子图,最后两个图是S0->S3激发主要牵扯到的分子轨道图。
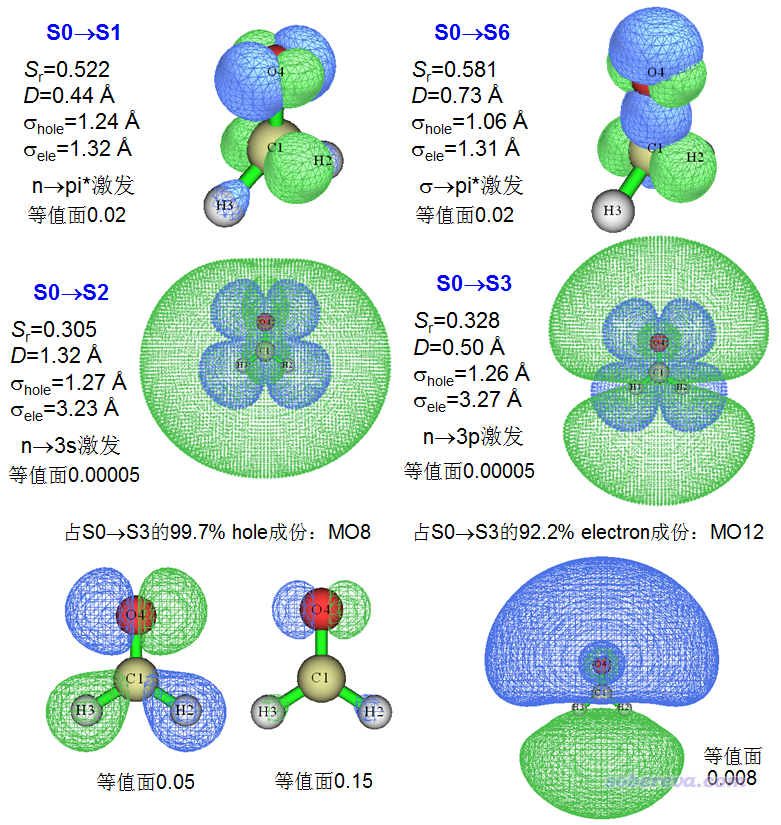
由图可见,S0->S1和S0->S6都是普通价层激发。像这样很小体系就无所谓局域激发和CT激发了,空穴和电子分布都有很大重叠,Sr都不算小。而且从σhole和σele指数来看,它们的空穴和电子的分布广度也差不多。根据空穴和电子的等值面形状,可以很容易想到主导的轨道是什么类型的,电子激发的主要特征也因此可以容易地指认。比如这两个电子激发的电子分布都是在C和O的分子平面两侧各有一个瓣,可想而知只有pi*轨道波函数对应的模的平方才有这种分布特征。如果感觉实在判断不出来,可以考察主导的MO的轨道等值面图来帮助判断。
上图的S0->S2和S0->S3一看空穴&电子等值面图就知道肯定是个里德堡激发,因为图上显示电子分布范围非常大,已经显著出现在了分子外围区域,且远远超过空穴的分布范围。这点也直接体现在电子的σ非常大,是空穴的σ的近三倍。从Sr上也体现出,由于空穴和电子的分布范围差异较大,Sr的数值比较小,显著小于S0->S1和S0->S6这样普通价层激发的情况。注意,上图中显示里德堡激发的空穴&电子图用的等值面数值很小,只有0.00005,这是因为这类激发的电子分布非常弥散,摊得非常开,如果等值面数值不这么小的话,就看不到电子对应的很弥散的等值面(可能有人觉得,对于价层激发,等值面数值用这么小的话电子的等值面照样也会很弥散,与里德堡激发不容易区分开。但别忘了,对于普通价层激发,当你把等值面数值设得很小的时候,空穴的等值面也会同时变得非常弥散,而里德堡激发的电子的等值面弥散程度总会远高于空穴的)。这俩里德堡激发的D指数不大,这从等值面图上也可以大致看出,确实空穴和电子的质心位置相差不是很大。本例体现出前面提到的里德堡激发应具备的特征是:D和S都不大,而电子的σ指数远大于空穴的。
实际上电子离域指数EDI也能充分区分价层激发和里德堡激发。价层激发S0->S1的HDI=24.8、EDI=17.0,而里德堡激发S0->S2的HDI=23.7、EDI=3.0,另一个里德堡激发S0->S3的HDI=23.9、EDI=2.8。可见里德堡激发的EDI远远小于价层激发。
了解里德堡激发的人,从上面给出的S0->S3的空穴&电子等值面图上已经可以指认出激发类型了。如果判断不出来,也可以让Multiwfn输出对空穴和电子贡献最大的MO,根据MO图形的相位,可以更容易地判断。此激发的空穴的几乎全部成分的是MO8,从上图左下角的0.05等值面图来看,既有氧的孤对电子特征,也有C-H sigma键特征。碰到这种难以指认的情况,可以尝试增大等值面数值,增大到0.15之后,可以看到等值面只剩下氧的孤对电子特征了,因此MO8最主体的特征就是氧的孤对电子。对S0->S3的电子贡献最大的是MO12,达到92.2%,可以说是绝对主导了。从其轨道图形可见(用了较小等值面数值以使其弥散特征可以充分展现),它在分子两侧有相位相反的两个瓣,类似p原子轨道特征,而当前分子的占据的原子轨道当中最高主量子数为2,因此MO12可以说是3p轨道。故S0->S3可以指认为n->3p型里德堡激发。而S0->S2则应指认为n->3s型里德堡激发,因为其电子分布接近球形,必然主要是s型这种几乎球对称的里德堡轨道主要贡献的。
5 技巧:通过脚本批量做空穴-电子分析得到一批激发态的各种指数
将Multiwfn和Linux的shell脚本结合使用,可以轻易实现一条命令就把所有激发态的各种指数全都算出来的目的。比如,我们想把4.1节的那个D-pi-A体系的S0->S1,S2,S3激发态的各种指数全都一次性算出来,那么创建一个文本文件,比如叫batch.sh,然后把以下内容拷进去(此文件在本文的文件包里也有):
#!/bin/bash
cat << EOF > calcall.txt
18
1
D-pi-A.out
EOF
for ((i=1;i<=3;i=i+1)) #Range of excited states
do
cat << EOF >> calcall.txt
$i
1
2
0
0
1
EOF
done
./Multiwfn D-pi-A.fchk < calcall.txt |tee out.txt #Running command
rm ./calcall.txt ./result.txt -f
grep "Sr index" ./out.txt |nl >> result.txt;echo >> result.txt
grep "D index" ./out.txt |nl >> result.txt;echo >> result.txt
grep "RMSD of hole in" ./out.txt |nl >> result.txt;echo >> result.txt
grep "RMSD of electron in" ./out.txt |nl >> result.txt;echo >> result.txt
grep "H index" ./out.txt |nl >> result.txt;echo >> result.txt
grep "t index" ./out.txt |nl >> result.txt
echo
echo "Finished!"
这个脚本在《详谈Multiwfn的命令行方式运行和批量运行的方法》(http://sobereva.com/612)中专门做了特别详细的介绍。简单来说,就是先产生一个calcall.txt文件,这里面包含了在Multiwfn里对S0->S1、S0->S2、S0->S3的空穴-电子分析所需要敲入的全部指令,其中利用到了循环,for ((i=1;i<=3;i=i+1))这个地方的i=1就是第一个激发态的序号,i<=3对应的是最后一个要算的激发态的序号。然后,脚本通过silent方式调用Multiwfn进行计算,输出文件out.txt里包含了Multiwfn的所有输出信息。最后用grep命令把感兴趣的信息从里面全都提取出来并写入到result.txt里。|nl用来对每批提取的信息加行号,便于与激发态序号对应(假设算的第一个态是第1激发态的话)。
把batch.sh、D-pi-A.fchk、D-pi-A.out都拷到Multiwfn所在目录下,然后在终端里进入此目录,运行chmod +x ./batch.sh给这个脚本加可执行权限,然后输入./batch.sh运行此脚本。运算过程中Multiwfn的运行状态也会在屏幕上显示,最后屏幕上出现Finished!的时候就算完了。然后打开当前目录下新生成的result.txt,内容如下
1 Sr index (integral of Sr function): 0.51896 a.u.
2 Sr index (integral of Sr function): 0.64906 a.u.
3 Sr index (integral of Sr function): 0.54538 a.u.
1 D_x: 0.522 D_y: 0.001 D_z: 0.001 D index: 0.522 Angstrom
2 D_x: 3.481 D_y: 0.007 D_z: 0.025 D index: 3.481 Angstrom
3 D_x: 0.574 D_y: 0.001 D_z: 0.001 D index: 0.574 Angstrom
1 RMSD of hole in X/Y/Z: 1.443 1.160 0.437 Norm: 1.902 Angstrom
2 RMSD of hole in X/Y/Z: 3.055 0.826 0.740 Norm: 3.251 Angstrom
3 RMSD of hole in X/Y/Z: 0.984 1.032 0.416 Norm: 1.486 Angstrom
略...
可见,感兴趣的信息都提取出来了。大家可以根据实际需要自己修改脚本,比如可修改里面积分格点质量的设定(目前的是中等质量格点,要改的话改$i下面第二行)、对延展距离进行设定等。使用脚本实在超级方便!
如果想把每个激发态的各种格点数据分别导出也很容易。比如我们想得到每个态的密度差格点数据CDD.cub,就将上面的从$i到EOF部分的内容改为
$i
1
2
0
-1 <---- 让导出的格点数据文件名末尾加上当前的激发态的序号
15 <---- 导出密度差格点数据
0
1
EOF
运行脚本后,比如第5个激发态的密度差格点数据就是当前目录下的CDD_00005.cub。
6 关于Δr指数
Δr指数虽然和空穴-电子分析在计算形式上没直接关系,但是和此文讨论的问题有较大联系,因此这里专门提一下,详细说明见Multiwfn手册3.21.4节。Δr是Adamo等人在J. Chem. Theory Comput., 9, 3118 (2013)中提出的,定义如下
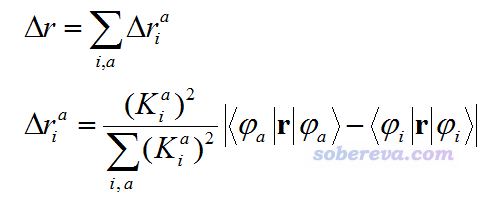
其中的K=w+w',即激发组态和去激发组态系数之和。Δr被原作者用来考察CT程度,被认为Δr越大CT程度越高。从定义上看,Δr指数的思想是每一对轨道跃迁的质心距离做权重加和,式中诸如<φ_a|r|φ_a>就相当于a轨道的质心位置,而|<φ_a|r|φ_a>-<φ_i|r|φ_i>|就相当于i与a轨道间跃迁对应的轨道质心距离,而前头的K^2/∑K^2项就相当于i-a轨道跃迁在电子激发中的权重。
从物理意义上看,其实Δr指数和D指数比较接近,本质上都是衡量空穴和电子的质心距离,但D指数的计算形式是严格的,而Δr指数的物理意义则没那么好,而且也没考虑到组态函数之间的耦合,因此一般没必要用Δr指数指数。当你发现D指数和Δr指数有明显冲突的时候,也应当以D指数为准。但Δr指数有一个好处是计算非常快,而且在Multiwfn中可以一次对一大批激发态计算出来,都不需要利用脚本,而且Δr指数还可以分解为轨道跃迁的贡献,这在上面的公式中已经体现了。
在Multiwfn中计算Δr指数指数所需的输入文件和空穴-电子分析完全一样。比如对4.1节的D-pi-A体系,要计算Δr指数,就在Multiwfn启动后输入如下命令:
D-pi-A.fchk
18
4 //计算Δr指数
D-pi-A.out
1-5 //要计算的激发态序号。1-5代表计算S0到所有5个激发态
结果如下,瞬间就算出来了,Δr单位是距离,以两种单位分别输出
Excited state 1: Delta_r = 4.607326 Bohr, 2.438092 Angstrom
Excited state 2: Delta_r = 9.456166 Bohr, 5.003988 Angstrom
Excited state 3: Delta_r = 4.075887 Bohr, 2.156867 Angstrom
Excited state 4: Delta_r = 3.940624 Bohr, 2.085289 Angstrom
Excited state 5: Delta_r = 2.776245 Bohr, 1.469126 Angstrom
通过对比可以发现,对当前体系,Δr和D指数确实存在正相关性,体现出二者的内在特征的相似性;而Δr和Sr指数则基本没有相关性,毕竟它俩在定义上没有明显相似之处。
如果选择要考察的激发态序号的时候只选择了一个轨道,Multiwfn就可以把Δr分解为各个轨道对的贡献,这在某些情况下可以把问题研究更得深入。例如对上述D-pi-A体系,选择要考察的激发态序号的时候输入4选择激发态S4,然后屏幕上输出Δr指数后会问你是否输出轨道对的贡献,此时输入y,然后输入显示阈值,这里输入0.01,程序就把对Δr指数贡献超过0.01埃的都输出出来了,如下所示:
#Pair Orbitals Coefficient Contribution (Bohr and Angstrom)
2516 52 57 -0.1175600 0.1053200 0.0557330
2517 52 59 -0.0438400 0.0364131 0.0192690
2592 53 57 0.1450600 0.2444716 0.1293688
2785 56 57 0.6318800 8.7878820 4.6503472
2787 56 59 -0.1128900 0.1361715 0.0720588
其中#Pair是相应轨道跃迁对应的单激发组态函数的序号,不用管。由数据可见,之所以S0->S2的Δr高达5.00埃,主要是因为56与57轨道之间的跃迁(显然分别对应HOMO和LUMO)贡献了多达4.65埃。
7 关于Λ指数
最早提出的,而且也是目前使用得很多的考察电子激发特征的指数是J. Chem. Phys. 128, 044118 (2008)中提出的Λ指数,Δr指数其实就是在上面做了鸡毛蒜皮的修改。Λ指数和Δr指数形式极其相似,把Δr指数中的|<φ_a|r|φ_a>-<φ_i|r|φ_i>|项替换为∫|φ_a||φ_i|dr(相当于衡量a,i两个轨道的重叠程度)就是Λ指数。Multiwfn中的主功能18的子功能14可以计算Λ指数,计算过程和Δr指数指数如出一辙,就不在这里示例了,手册4.18.4节有例子,在手册3.21.14节里有详细说明。
Λ指数的计算比Δr更耗时,因为其中牵扯到的轨道波函数模的乘积的积分需要通过数值格点方式来积分。但Multiwfn中计算Λ指数的功能已经做了最大程度的优化,因此对大体系的实际耗时还是完全可以接受的。如果认为Δr是D的“劣化”版,那么可以将Λ指数视为是Sr指数的“劣化”版。从本质上看,Λ指数和Sr指数都是对空穴与电子重叠程度的体现,但Λ指数并没有Sr指数在定义上那么严格,而且也忽视了组态间的耦合。凡是Λ指数和Sr指数存在冲突的情况,也都应当用Sr指数说事。
正如同D和Sr指数存在明显的互补作用,对实际问题分析缺一不可,倘若你有特殊原因非要用Δr和Λ来说事,也不要只使用其一,最好结合使用,以便对电子激发特征了解得更全面。
还有其他一些人提出的各种各样的表征电子激发的特征指数,比如J. Chem. Theory Comput., 10, 3896 (2014)提出的φs指数。由于Multiwfn里支持的考察电子激发特征的指数已经足够充分了,已经可以把电子激发研究得极尽透彻了,因此我就不再打算在Multiwfn里加入乱七八糟没多大用处的其它的指数了。
8 总结
本文全面、系统地介绍了Multiwfn中强大的空穴-电子分析功能,仔细阅读过本文的读者应该已经认识到这对于考察电子激发问题是必不可少的利器,可以把电子激发特征从各个角度一览无余地剖析透彻,既能给出详实的定量数据,又能给出漂亮的吸引眼球的图像。本文虽然只用了三个简单体系举例,就已经讨论出相当多的信息了,而且这还仅仅是Multiwfn支持的全部电子激发分析方法中的一部分。可见,经常研究电子激发问题的人,若充分灵活运用Multiwfn,特别是空穴-电子分析,还愁文章里没得讨论?