在Multiwfn中基于fch产生自然轨道的方法与激发态波函数、自旋自然轨道分析实例
在Multiwfn中基于fch产生自然轨道的方法与激发态波函数、自旋自然轨道分析实例
The way of generating natural orbitals based on fch file in Multiwfn and analysis instances about excited state wavefunctions and spin natural orbitals
文/Sobereva @北京科音
First release: 2018-Jan-8 Last update: 2020-Nov-6
0 前言
在《详谈Multiwfn支持的输入文件类型、产生方法以及相互转换》(http://sobereva.com/379)和Multiwfn手册第四章开头都说过,对于Gaussian用户,如果要在Multiwfn中分析后HF波函数、TDDFT激发态波函数或者双杂化泛函的波函数,需要产生相应级别的自然轨道并让Multiwfn载入。自然轨道可以让Gaussian以.wfn/wfx形式输出,也可以让Gaussian将之存到.fch里。前者很容易,但此类输入文件在Multiwfn里没法进行需要利用基函数信息的分析(如Mayer键级、Mulliken电荷);后者虽然没这个限制,但是导出过程很繁琐,需要Gaussian中运行两步,要用的关键词容易忘,而且之后还得在.fch开头自行填上saveNO。fch文件里是包含密度矩阵信息的,自然轨道也正是通过对角化密度矩阵得到的。但fch里的密度矩阵不会被Multiwfn所直接利用,Multiwfn从输入文件里只会读取轨道信息。从2018-Jan-7更新的Multiwfn开始,为了方便用户,笔者在Multiwfn中添加了一个功能,可以读取fch里的密度矩阵并产生各类自然轨道。本文目的是说一下相关细节,演示一下怎么用,并顺带简要讲一下激发态波函数的分析和自旋自然轨道的分析。
1 关于fch里的密度矩阵和自然轨道
在chk里,以及转换出的fch文件里,至少包含了SCF级别的密度矩阵,对于后HF、双杂化泛函、TDDFT等任务,还会包含其它类型密度矩阵(前提是用了density或某些特殊关键词,而且当前理论方法在Gaussian中有解析梯度)。在fch文件里搜索Density就能知道包含哪些。这里罗列一下常见情况:HF、DFT、CASSCF任务:SCF
CIS、TDDFT任务:CI、CI Rho(1)
CCSD任务:CC
MP2、双杂化泛函任务:MP2
MP3任务:MP3
MP4SDQ任务:MP4
如果你的体系是开壳层(对于CIS/TD来说指的是参考态),还会包含自旋密度矩阵。比如,对一个三重态体系,如果你用的是比如# MP2/cc-pVDZ density关键词,则fch文件里会有这几个字段:
Total SCF Density:HF级别的总密度矩阵
Spin SCF Density:HF级别的自旋密度矩阵
Total MP2 Density:MP2级别的总密度矩阵
Spin MP2 Density:MP2级别的自旋密度矩阵
如果体系是闭壳层,就没有Spin SCF Density和Spin MP2 Density了。
所谓总密度矩阵,就是指Alpha和Beta密度矩阵的加和;而自旋密度矩阵,就是Alpha密度矩阵减去Beta密度矩阵。
Multiwfn能产生的自然轨道有三类,和密度矩阵的关系如下:
(a)自然轨道(Natural orbital, NO):对总密度矩阵对角化得到。本征值是占据数,原则上范围是0.0~2.0,本征矢就是自然轨道系数。这种自然轨道也被称为Spatial natural orbital,因为不含自旋信息。如果体系是开壳层的,这种自然轨道也被确切叫做unrestricted natural orbital (UNO)。
(b)Alpha自然轨道、Beta自然轨道:分别对Alpha密度矩阵和Beta密度矩阵对角化得到,分别描述Alpha和Beta电子,原则上占据数在0.0~1.0之间。这类自然轨道也被称为自然自旋轨道(natural spin orbital, NSO)。
(c)自旋自然轨道(Spin natural orbital, SNO):对自旋密度矩阵对角化得到,占据数在-1.0至1.0之间。占据数为正和为负的SNO分别描述Alpha单电子和Beta单电子。
2 实例1:分析甲醛TDDFT计算的S1态波函数
运行以下输入文件,对甲醛在TD-PBE0/6-31G*级别下做电子激发计算,并且把S1态密度矩阵存到chk里(因为TD里的root选项默认为1)。%chk=C:\H2CO.chk
# PBE1PBE/6-31G* TD density
B3LYP/6-31G* opted
0 1
C 0.00000000 0.00000000 -0.56221066
H 0.00000000 -0.92444767 -1.10110537
H -0.00000000 0.92444767 -1.10110537
O 0.00000000 0.00000000 0.69618930
用formchk将chk转换为fch,里面此时会有Total SCF Density、Total CI Rho(1) Density、Total CI Density三个字段,分别对应于基态DFT密度矩阵、TDDFT非弛豫的S1态密度矩阵(可无视)、TDDFT弛豫的S1态密度矩阵。
下面我们来考察一下S1态的C-O Mayer键级以及O的ADCH原子电荷。启动Multiwfn,依次输入
H2CO.fch
200
16 //基于fch里的密度矩阵产生自然轨道
CI //载入的密度矩阵级别
由于输入的是CI,所以Multiwfn从fch中读取了Total CI Density字段记录的S1态总密度矩阵,并立刻产生了相应的S1态自然轨道,占据数直接输出在屏幕上了(占据数稍微超过理论上0.0~2.0范围是正常情况,不用纠结):
Occupation numbers:
2.033734 2.002238 2.000812 2.000459 2.000148 2.000000
2.000000 0.996739 0.970938 0.000094 0.000062 0.000049
0.000019 0.000005 0.000002 0.000000 0.000000 0.000000
0.000000 0.000000 -0.000000 -0.000000 -0.000000 -0.000000
-0.000000 -0.000000 -0.000000 -0.000000 -0.000238 -0.000366
-0.000454 -0.000828 -0.001168 -0.002245
此时,内存里的基函数信息已经被更新成了对应S1自然轨道的情况了,做各种基于基函数的分析的结果将是对应S1态的了。我们还要计算ADCH电荷,这是要用GTF信息的,但目前GTF系数还是对应基态DFT轨道的的(因为一开始载入的.fch里的轨道是基态DFT的),且现在轨道占据数已经变成了自然轨道占据数,所以之后做基于GTF信息的分析将没有任何物理意义。为了能计算S1态的ADCH电荷,我们此时应当选y,让程序把当前的波函数信息导出为当前目录下的new.mwfn,并自动载入之,此时内存里的GTF信息也变成对应S1态的了。这个new.mwfn文件我们以后也再可以反复利用。
接着输入以下内容
0 //退回主菜单
9 //键级计算
1 //Mayer键级
得知C-O键级为1.18。然后输入
n //不导出键级矩阵
0 //退回主菜单
7 //布居分析
11 //ADCH电荷
1 //用内置的球对称化的自由原子密度
得知O的ADCH电荷为-0.128。
我们可以对比一下基态的情况。重启Multiwfn,载入H2CO.fch,此时内存里的基函数信息和GTF信息都是对应基态的,重做上述计算,发现C-O Mayer键级为1.98,O的ADCH电荷为-0.296。
之所以激发态的C-O键级比基态的小得多,激发态的O的电荷也比基态的正得多,是因为此激发是n->pi*激发,一方面削弱了C-O键,一方面一部分电子从氧转移给了C。
3 实例2:分析丁烷双自由基的自旋自然轨道
丁烷双自由基体系在《CASSCF计算双自由基以及双自由基特征的计算》(http://sobereva.com/264)中做了很详细的讨论,建议看看。本节的例子探究一下此体系的SNO轨道。
运行以下输入文件
%chk=C:\C4H8.chk
#p UB3LYP/def2SVP guess=mix nosymm
ub3lyp/6-31g(d) opted
0 1
C -0.74400100 1.78566400 0.00000000
H -0.60282700 2.33865300 0.92499500
H -0.60282700 2.33865300 -0.92499500
C -0.74400100 0.30988100 0.00000000
H -1.25452600 -0.08746700 0.88463900
H -1.25452600 -0.08746700 -0.88463900
C 0.74400100 -0.30988100 0.00000000
H 1.25452600 0.08746700 -0.88463900
H 1.25452600 0.08746700 0.88463900
C 0.74400100 -1.78566400 0.00000000
H 0.60282700 -2.33865300 -0.92499500
H 0.60282700 -2.33865300 0.92499500
将chk转换成fch后,启动Multiwfn,依次输入
C4H8.fch
200
16
SCF //考察DFT级别的密度矩阵
此时程序问你,是产生空间自旋轨道(此时叫做UNO),Alpha和Beta各自的自然自旋轨道(NSO),还是自旋自然轨道(SNO)。我们选3产生SNO,看到的占据数如下
0.957908 0.045983 0.043627 0.037531 0.021487 0.021280
0.020200 0.017324 0.008494 0.007915 0.006743 0.006539
0.000626 0.000604 0.000082 0.000082 0.000000 0.000000
...略
-0.000000 -0.000000 -0.000082 -0.000082 -0.000604 -0.000626
-0.006539 -0.006743 -0.007915 -0.008494 -0.017324 -0.020200
-0.021280 -0.021487 -0.037531 -0.043627 -0.045983 -0.957908
可见占据数为正的SNO当中只有一个数值较大的,即第一个(0.9579);而占据数为负的SNO当中也只有一个数值较大的,即最后一个(-0.9579)。而且,我们也知道,由于此体系是个很理想的双自由基体系,本来就应该有一个Alpha和一个Beta单电子。因此,未成对的Alpha电子和Beta电子分布特征通过考察这两个轨道就足够得知了。
我们选y产生new.mwfn并自动载入之,然后进入主功能0观看这两个轨道的特征。值得一提的是,new.mwfn被Multiwfn视为是开壳层的,因此形式上会有Alpha和Beta两套轨道,而我们产生的SNO轨道只有一套,此时SNO轨道占用的是用于记录Alpha轨道那部分空间(绝对不是说SNO的物理意义是Alpha轨道),而Beta轨道那部分没有意义,占据数也都是0。我们在主功能0的界面里可以选左上角的Orbital info.,从文本窗口里找出占据数为0.957908和-0.957908的轨道,可知序号分别是1和96(其实96就是体系的基函数数目,因此都没必要去列表里找,直接选就行),这两个轨道的图形如下:
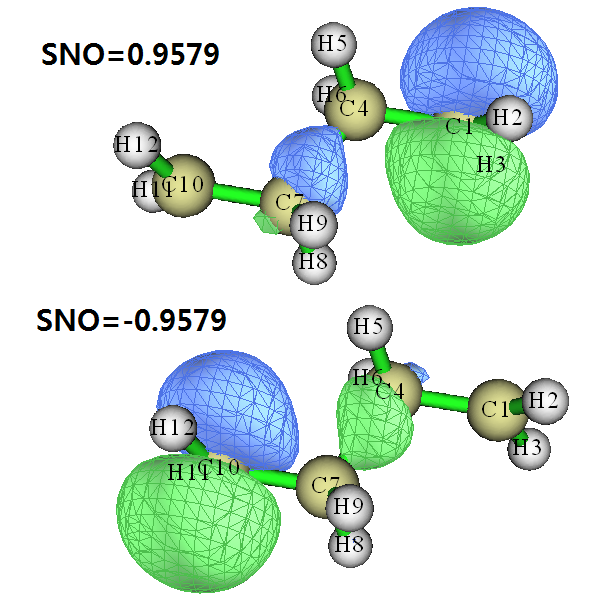
可见,Alpha单电子主要分布在C1上,在C4-C7之间也有少量分布。Beta单电子主要分布在C10上,同样在C4-C7之间也有少量分布。
如果我们想定量知道比如Alpha单电子在各个原子上的量,我们可以对主要表现Alpha单电子的SNO1做轨道成分分析。我们回到主菜单,依次输入
8 //轨道成分分析
8 //Hirshfeld方式做轨道成份分析
1 //用内置的球对称化的自由原子密度
1 //1号轨道
结果为
Atom 1(C ) : 70.148760%
Atom 2(H ) : 6.317230%
Atom 3(H ) : 6.317230%
Atom 4(C ) : 7.588237%
Atom 5(H ) : 1.254212%
Atom 6(H ) : 1.254212%
Atom 7(C ) : 5.065489%
Atom 8(H ) : 0.591654%
Atom 9(H ) : 0.591654%
Atom 10(C ) : 0.758644%
Atom 11(H ) : 0.056339%
Atom 12(H ) : 0.056339%
数值和我们从轨道图形上看到的很好相符。
众所周知,研究单电子分布最常用的方法是分析自旋密度。我们重新载入C4H8.fch,绘制一下自旋密度图,步骤见《谈谈自旋密度、自旋布居以及在Multiwfn中的绘制和计算》(http://sobereva.com/353),图像如下:
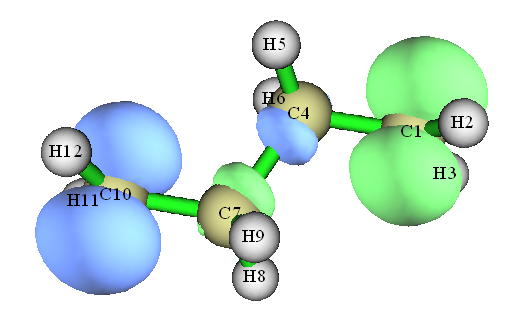
我们再用主功能15,在Hirshfeld划分下计算自旋密度在各个原子空间中的积分值(原子自旋布居):
Atomic space Value
1(C ) 0.70928760
2(H ) 0.04488357
3(H ) 0.04488357
4(C ) -0.01371421
5(H ) 0.00849956
6(H ) 0.00849956
7(C ) 0.01371421
8(H ) -0.00849956
9(H ) -0.00849956
10(C ) -0.70928760
11(H ) -0.04488357
12(H ) -0.04488357
无论是从等值面图上,还是原子自旋布居上,都看到自旋密度分布特征基本等于主要描述Alpha单电子的SNO1和主要描述Beta单电子的SNO96特征的叠加。对于两个SNO基本没有重叠的体系两端的亚甲基的碳,其自旋布居和它对SNO的贡献量十分接近,而在C4、C7部分,由于两个SNO重叠厉害,导致显著的相互抵消,所以它们虽然对SNO贡献不很小,但是自旋布居却非常小。
可见,分析SNO的好处是可以分别考察未成对的Alpha和Beta电子原本是怎么分布的,且可以从轨道分析的角度研究;而考察自旋密度,则便于了解在Alpha和Beta单电子分布发生一定程度抵消后的单电子“净”分布情况,分析也更为省事,不用讨论多个轨道。两种分析是互补的。