使用Sobtop超级方便地创建二茂铁的GROMACS的拓扑文件
使用Sobtop超级方便地创建二茂铁的GROMACS的拓扑文件
Using Sobtop to create GROMACS topology file for ferrocene super conveniently
文/Sobereva@北京科音 2022-Feb-17
0 前言
Sobtop是笔者开发的主要用于产生各种类型体系的GROMACS拓扑文件的程序,可以在主页http://sobereva.com/soft/Sobtop免费下载。过渡金属配合物体系的拓扑文件在以往是很难产生的一类情况,因为里面牵扯到GAFF、OPLS-AA、GROMOS等主流有机分子力场不支持的元素,里面涉及到的键/键角/二面角参数在那些力场里也没有,所以acpype、Ligpargen、ATB等程序根本没法搞。而这类体系,用Sobtop则可以超级容易地产生拓扑文件。AmberTools里的MCPB.py程序虽然能产生这类体系的拓扑文件,但是过程麻烦至极,在http://bbs.keinsci.com/thread-27796-1-1.html里有人演示了怎么借助MCPB.py产生二茂铁的GROMACS的拓扑文件,估计大多数人看了后会打退堂鼓。Sobtop的详情以后会另文专门系统性地介绍,本文仅简单演示一下怎么用Sobtop快捷地产生二茂铁的拓扑文件,通过对比大家可以充分认识到用Sobtop有多么方便。
本文牵扯到的所有输入输出文件都可以在http://sobereva.com/attach/635/file.rar里找到。Sobtop用的是2022-Feb-16发布的预览版1.0(dev)。Multiwfn用的是2022-Feb-17更新的版本,Multiwfn可以在主页http://sobereva.com/multiwfn免费下载。
1 用Gaussian做优化和振动分析
首先用Gaussian对二茂铁做优化和振动分析。要注意,二茂铁的两个茂环间仅在低温晶体中是交错式的,而在真空中极小点结构是重叠式的(参看Materials, 8, 7723 (2015)和https://en.wikipedia.org/wiki/Ferrocene#Determining_the_structure中的相关信息),因此本例用重叠式(D5h点群)的初始结构。记得Gaussian计算前最好用GaussView做对称化,这样优化得又精准速度又快。
关于计算级别,本例用的TPSSh/def2-TZVP级别对于过渡金属配合物体系通常是很理想的选择。关于泛函的选择看《简谈量子化学计算中DFT泛函的选择》(http://sobereva.com/272)。如果想明显更便宜,Fe可以用SDD,配体可以用6-311G*。
此例的Gaussian输入文件如下
%chk=Ferrocene.chk
#p tpssh/def2tzvp opt freq
[空行]
Generated by Multiwfn
[空行]
0 1
C 0.71056100 -0.97800331 1.65426528
C -0.00000000 1.20887857 1.65426528
C -0.71056100 -0.97800331 1.65426528
H 2.17848562 0.70783289 1.62195576
H -2.17848562 0.70783289 1.62195576
Fe 0.00000000 0.00000000 -0.00000000
C 1.14971184 0.37356402 1.65426528
C -1.14971184 0.37356402 1.65426528
H 1.34637816 -1.85313055 1.62195576
H -0.00000000 2.29059533 1.62195576
H -1.34637816 -1.85313055 1.62195576
C 1.14971184 0.37356402 -1.65426528
C -1.14971184 0.37356402 -1.65426528
C 0.71056100 -0.97800331 -1.65426528
C 0.00000000 1.20887857 -1.65426528
C -0.71056100 -0.97800331 -1.65426528
H 2.17848562 0.70783289 -1.62195576
H -2.17848562 0.70783289 -1.62195576
H 1.34637816 -1.85313055 -1.62195576
H 0.00000000 2.29059533 -1.62195576
H -1.34637816 -1.85313055 -1.62195576
[空行]
[空行]
算完了之后,用formchk把当前目录下的Ferrocene.chk转换为Ferrocene.fchk。不知道formchk是什么和怎么用的话看《详谈Multiwfn支持的输入文件类型、产生方法以及相互转换》(http://sobereva.com/379)里相关部分。
还需要得到二茂铁的mol2文件,并且要求其中记录的键连关系和期望的一致,这决定了Sobtop给出的拓扑文件里都有哪些力场项。很多程序都可以实现这个,此例我们用常用的GaussView打开Ferrocene.fchk,如果看到Fe和各个C之间没显示键的话就手动连上(设几重键都无所谓,Sobtop只看有没有键)。然后保存为Ferrocene.mol2。
2 计算RESP电荷
RESP电荷很适合用于动力学模拟的目的,我们要让拓扑文件里的原子电荷对应RESP电荷。计算RESP电荷非常强大、方便、灵活的程序是Multiwfn,见《RESP拟合静电势电荷的原理以及在Multiwfn中的计算》(http://sobereva.com/441)。要注意对二茂铁体系不宜直接按照常规方式算RESP电荷,因为拟合点的分布不会恰好满足D5h对称性,因此得到的等价原子的原子电荷会有微小的偏差。为了让所有等价的原子的电荷都严格相同,在Multiwfn中计算RESP电荷时应当设置等价性。
启动Multiwfn,然后输入
Ferrocene.fchk
7 //计算原子电荷
18 //计算RESP电荷
5 //等价性约束设置
11 //根据点群自动判断等价性
a //根据整个体系的结构判断点群
y //当前屏幕上显示的点群确实是D5h,列出的原子等价性没错,所以这里输入y确认。然后当前目录下有了等价性设置文件eqvcons_PG.txt
q //返回
1 //从文本文件里读取等价性设置
eqvcons_PG.txt //刚才产生的文件
2 //开始一步式RESP电荷拟合
[回车] //程序提示Fe缺半径,按回车表示用推荐的半径
Multiwfn算RESP电荷效率很高,RESP电荷很快就产生了,从屏幕上给出的结果看确实原子电荷合理,而且满足等价性。按y把产生的原子电荷导出为当前目录下的Ferrocene.chg。
3 用Sobtop产生拓扑文件
启动Sobtop,然后依次输入
Ferrocene.mol2
7 //指定原子电荷
10 //从Multiwfn的chg文件中读取原子电荷
Ferrocene.chg
0 //返回
2 //产生GROMACS的.gro文件
[回车] //此时当前目录下产生了Ferrocene.gro
1 //产生GROMACS的拓扑文件
2 //优先用GAFF原子类型,缺的自动用UFF力场的。原子类型决定了拓扑文件里的LJ参数
2 //所有成键相关参数基于振动分析产生的fchk文件里的Hessian矩阵生成
Ferrocene.fchk //如果此文件和Ferrocene.mol2在相同目录下,此处直接按回车可以快捷载入
[回车] //在当前目录下产生Ferrocene.top
[回车] //在当前目录下产生Ferrocene.itp
现在拓扑文件在当前目录下出现了,Sobtop可以关了。现在可以打开itp文件看看内容,会看到没有任何问题,文件整齐干净,注释也特别清楚。
4 测试拓扑文件合理性
产生拓扑文件之后,我一般建议在真空下对这个体系跑一下动力学,根据模拟过程中结构变化情况大致判断拓扑文件是否合理。做这个模拟要用的Ferrocene.gro、Ferrocene.top、Ferrocene.itp前面我们都已经产生了。做这个模拟用的md.mdp在本文的文件包里也给了,可见是控温在298.15K下模拟100 ps,1 fs一步,每100 fs往xtc里写入一帧,没有用PBC。笔者此例用的是GROMACS 2018.8。这个mdp不兼容GROMACS较新版本,较新版本用户需要在一个足够大的空盒子里在考虑PBC的情况下跑NVT模拟。
把前述的gro、itp、top、mdp都放到当前目录下,运行以下命令
gmx grompp -f md.mdp -c Ferrocene.gro -p Ferrocene.top -o md.tpr
gmx mdrun -v -deffnm md
然后用VMD载入轨迹,用Extensions - Analysis - RMSD Trajectory Tool工具对system选区做align消除平动转动后,每10帧叠加显示一次,得到下图
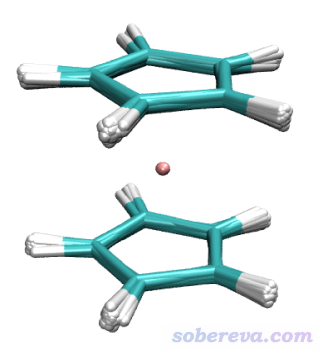
可见模拟过程中二茂铁很好地维持了刚性,说明拓扑文件合理。
5 总结&其它
本例充分体现了使用Sobtop结合Multiwfn程序产生过渡金属配合物体系拓扑文件的便利,把复杂度降低到了极限。此文只以极为简单的体系做了示例,对更复杂的情况,诸如多核金属配合物、除了刚性部分还带有可旋转键的柔性部分的配合物,Sobtop也都能很容易地产生拓扑文件。凡是体系全为刚性的情况都可以直接效仿本文的做法;对于既有刚性配位区域也有柔性基团的配合物,在Sobtop问你怎么产生成成键相关(bonded)参数时,建议选择相应选项,让bond和angle参数用特定方法基于Hessian产生,而其它的用预置力场参数,这样可以使得GAFF的参数用于描述柔性部分二面角可旋转特征。
实际中二茂铁的茂环的旋转势垒是非常低的,常温下是可以旋转的,但本文得到拓扑文件对应的是纯刚性二茂铁。本文暂不考虑茂环间可相对旋转的问题,这也不是什么重要问题。
本文的做法比起MCPB.py实在方便百倍,而且MCPB.py用的Seminario方法产生力常数也不如本文的方法合理(当前版本Sobtop默认用的是modified Seminario,产生的键角力常数远好于Seminario)。
做优化和振动分析用免费的ORCA亦可,文中用fchk的地方改成用ORCA振动分析产生的.hess文件即可。
对于体系没有对称性的情况,算RESP电荷时不需要本文这样做对称等价设置,直接在Multiwfn的RESP界面里选择1用常规的两步式拟合即可。更多细节看《RESP拟合静电势电荷的原理以及在Multiwfn中的计算》(http://sobereva.com/441)。
本文的例子直接从chg文件中载入了RESP电荷。也可以在Sobtop里先不设置电荷,等itp产生出来之后再手动把要用的电荷写入到[ atoms ]部分。
使用Sobtop产生拓扑文件发表文章时记得按照Sobtop主页http://sobereva.com/soft/Sobtop的说明进行引用。引用方式在未来会有所变化,请记得发文章之前看一下主页上最新的引用说明。