使用Multiwfn计算与超瑞利散射(HRS)实验相关的量
使用Multiwfn计算与超瑞利散射(HRS)实验相关的量
Using Multiwfn to calculate quantities related hyper-Rayleigh scatter experiment
文/Sobereva@北京科音
First release: 2019-Aug-7 Last update: 2020-Jun-26
摘要:超瑞利散射(HRS)是考察分子第一超极化率的一种实验手段,本文介绍如何使用Multiwfn基于Gaussian的polar任务的输出文件计算出与HRS实验相关的量。首先介绍基础知识,然后给出具体例子,并重复文献里的数据。
笔者参与的一篇文章中利用了Multiwfn将本文介绍的HRS分析用于了实际研究中,见J. Phys. Chem. A (2020) DOI: 10.1021/acs.jpca.0c03166,欢迎阅读和引用。
1 基本知识
之前笔者在《使用Multiwfn分析Gaussian的极化率、超极化率的输出》(http://sobereva.com/231)中已经对(超)极化率的相关知识和计算有过基本的介绍。实验上测定beta(第一超极化率)常用的方法是EFISHG(电场诱导二次谐波产生)实验,这个测的是平行于分子偶极矩的beta(-2w;w,w)的分量,这里w是外场频率。还有一种实验上考察beta(-2w;w,w)的方法是超瑞利散射(Hyper-Rayleigh Scattering, HRS),相关介绍见Acc. Chem. Res., 31, 675 (1998)(此文有个别错误)。HRS实验示意图如下。
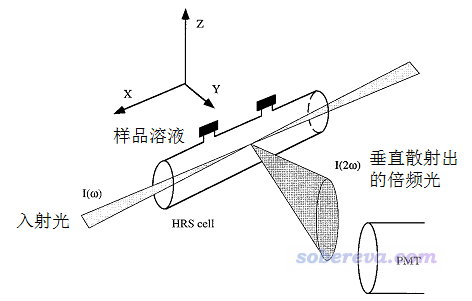
根据入射光的强度和测定的垂直散射出的倍频光的强度,可以得到beta_HRS值,表达式如下,它是对分子的beta(-2w;w,w)的一种展现,是各向平均属性,不受分子朝向的影响。其中<beta^2 ZZZ>和<beta^2 XZZ>的具体定义看Multiwfn手册3.200.7节或PCCP,10,6223(2008),是基于beta(-2w;w,w)张量的各个分量计算的。还有个量叫退偏比(depolarization ratio, DR),定义也在下面给出了,理论最小值为1.5(对应Td点群的分子)。
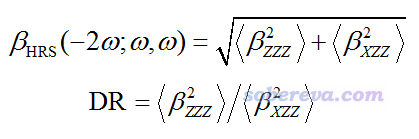
<beta^2 ZZZ>和<beta^2 XZZ>可分解为偶极(J=1)和八极(J=3)成份的加和,如下所示。并进而可以定义各向异性参数ρ,以及偶极和八极对beta的相对贡献φ(beta J=1)和φ(beta J=3)。
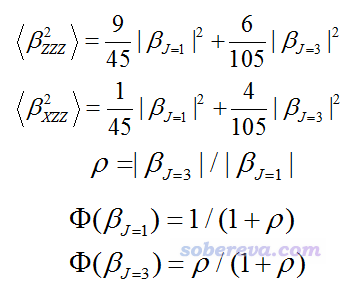
对于小分子,其偶极矩大小与上述很多量有密切联系,本文就不多说了,读者可参看J. Chem. Phys., 136, 024506 (2012)里的例子。
入射光的极化态通过(Ψ,δ)两个参数确定。当入射光以X方向射入、相位延迟量δ=π/2时,顺着Y方向散射出的沿Z方向极化的光的强度与入射光极化角Ψ的关系为:
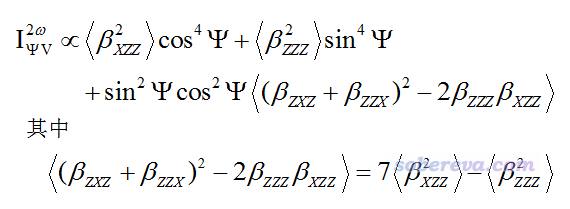
很多文章里都考察了散射光强度随Ψ的变化关系,比如JCP,136,024506(2012)、JPCA,116,10249(2012)。
2 用法&例子
下面就结合例子说一下用Multiwfn具体怎么计算前述的与HRS相关的量。注意从2019年7月30日更新的Multiwfn 3.7(dev)开始才有相关功能,绝对不要用在此日期之前发布的版本!!!Multiwfn可在其主页http://sobereva.com/multiwfn免费下载。
计算HRS相关的量需要提供Gaussian的polar=DCSHG任务的输出文件。此处我们重复一下JCP,136,024506(2012)中对CH2Cl2计算的结果。文中给了很多数据,我们这里将要对照文中在HF/d-aug-cc-pVTZ级别下结合IEFPCM描述CH2Cl2溶剂环境时算的数据,入射波长取的是1064nm。Gaussian的输入文件如下。
#p HF/daug-cc-pVTZ polar=DCSHG CPHF=rdfreq scrf=solvent=CH2Cl2
[空行]
Title Card Required
[空行]
0 1
C 0.00000000 0.00000000 0.76822500
H -0.89768500 0.00000000 1.37593000
H 0.89768500 0.00000000 1.37593000
Cl 0.00000000 1.49574000 -0.21650600
Cl 0.00000000 -1.49574000 -0.21650600
[空行]
1064nm
这个例子里,#P必须有,否则Multiwfn无法解析输出文件。d-aug-cc-pVTZ在Gaussian里写作daug-cc-pVTZ。由于HRS展现的是分子的beta(-2w;w,w),显然必须用polar=DCSHG关键词来计算这种形式的beta。CPHF=rdfreq结合末尾空一行处的1064nm代表要算的不仅有静态极限w=0的情况还有w=1064nm的情况(由于polar=DCSHG关键词默认了CPHF=rdfreq,因此CPHF=rdfreq也可以不写)。scrf=solvent=CH2Cl2代表用默认的IEFPCM隐式模型描述CH2Cl2溶剂环境。上面输入文件里的坐标是笔者事先使用与JCP文章里相同的级别优化好的。
上面的输入文件和G09 E.01计算产生的输出文件可以直接在此下载:http://sobereva.com/attach/499/file.rar。
启动Multiwfn,载入上述任务的输出文件CH2Cl2_solv.out,然后依次输入
200 //主功能200
7 //解析Gaussian的polar任务的输出文件里的(超)极化率信息并计算相关数据
-1 //切换为载入含频(超)极化率的模式
1 //当前用的计算级别是有解析三阶导数的级别,包括HF、普通DFT泛函、半经验
2 //载入对应w=1064nm的数据
2 //考察的形式是beta(-2w;w,w)
此时在屏幕上看到下面的输出
[beta各个分量略...]
Beta_X= 0.00000 Beta_Y= 0.00000 Beta_Z= 41.77407
Magnitude of first hyperpolarizability: 41.774067
Projection of beta on dipole moment: 41.774067
Beta || : 25.064440
Beta ||(z) : 25.064440
Beta _|_(z) : 8.334480
Note: Kleinman's symmetry condition is not employed for below quantities:
<beta_ZZZ^2>: 3.32226140E+02
<beta_XZZ^2>: 1.05032972E+02
Hyper-Rayleigh scattering (beta_HRS): 20.911
Depolarization ratio (DR): 3.163
|<beta J=1>|: 32.374
|<beta J=3>|: 46.322
Nonlinear anisotropy parameter (rho): 1.431
Dipolar contribution to beta, phi_beta(J=1): 0.411
Octupolar contribution to beta, phi_beta(J=3): 0.589
< (beta_ZXZ+beta_ZZX)^2 - 2*betaZZZ*betaZXX >: 4.03004664E+02
前文提到的beta_HRS值、<beta_ZZZ^2>、DR等各个量都已经明确给出来了。由于计算前没要求程序切换成其它单位输出,所以单位用的都是默认的a.u.。
在前述的JCP文章的表5中的最后一行我们看到在当前计算条件下beta_HRS值为20.90,DR值为3.12,我们自己算的结果分别是20.911和3.16,可见与文献高度相符。
如果你想考察散射光强度随Ψ的变化,此时输入y,然后输入一个起始角度。如果输入的值为r,那么就会给出Ψ从r到r+360度范围内每隔1度对应的散射光强度值。这里我们输入-180,然后屏幕上提示HRS_angle.txt已经导出到了当前目录下。内容为:
-180.0 105.032972
-179.0 105.091742
-178.0 105.268017
...略
177.0 105.561698
178.0 105.268017
179.0 105.091742
之后可以把这个文件拖入到Origin里并绘制成曲线图。由于当前的数据是360度周期性的,很多研究者通过图像展现这类数据的时候喜欢绘制成极坐标的图。具体做法是选择Plot - Polar theta(X)r(Y),然后对图像做一番调整,就可以得到下图的效果。相应的Origin的.opj文件在上面提到的文件包里直接提供了。
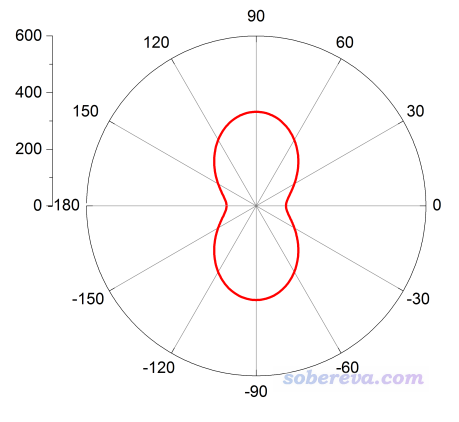
此图很容易理解,角度对应Ψ值,每个特定角度下红线距离原点的距离就是这个Ψ值对应的散射强度值。在前述JCP文章的图9里,给了与上图相对应的图,曲线图也一并给出,如下所示。其中右图中绿色长虚线对应的是我们上面用的计算级别,可见我们的图和文献里的图完全一致。
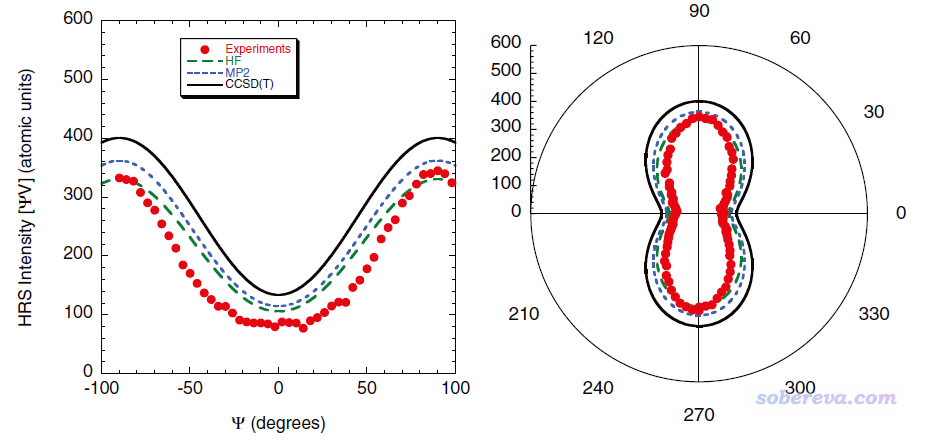
顺带一提,之前密度泛函小卒写过一个基于Python的程序NLO Calculator也可以计算上述这些量,Multiwfn计算的结果和NLO Calculator是一样的,但输出格式明显不同。