使用Multiwfn分析Gaussian的极化率、超极化率的输出
使用Multiwfn分析Gaussian的极化率、超极化率的输出
Using Multiwfn to analyze the polarizability and hyperpolarizability outputted by Gaussian
文/Sobereva @北京科音
First release: 2014-Apr-27 Last update: 2023-Aug-11
1 前言
Gaussian中polar关键词是专门用来计算极化率α和第一超极化率β的,从Gaussian09 D.01开始也支持polar=gamma计算第二超极化率γ。Gaussian输出的很多信息总是令初学者很难看懂,(超)极化率的输出更是如此,内容杂乱,而且不同理论方法下输出的信息格式还差异很大,分析起来很不方便。Multiwfn的主功能24里的子功能1就是专门用来解析Gaussian的(超)极化率的输出的,使之简洁易懂。与此同时,Multiwfn还会计算一些对于分析(超)极化率十分重要的量,比如<α>、α的各向异性值、β在分子偶极矩方向的分量等等,这使得通过Gaussian研究(超)极化率变得方便得多。此文的目的就是介绍如何使用Multiwfn分析Gaussian的(超)极化率的输出。
顺带一提,在笔者讲授的北京科音中级量子化学培训班(http://www.keinsci.com/KBQC)中专门有一节“(超)极化率的计算”,极其详尽和细致讲解(超)极化率的计算所涉及的各种相关背景知识和实际计算方法,十分推荐需要做这部分计算的读者参加。
本文内容对应的是Multiwfn官网上的最新版本,可以在其主页http://sobereva.com/multiwfn上免费下载,不要用老版本。Multiwfn是最强大的波函数分析程序,此文介绍的只不过是它的一个附属功能而已。如果对Multiwfn不熟悉,建议阅读《Multiwfn FAQ》(http://sobereva.com/452)和《Multiwfn入门tips》(http://sobereva.com/167)。Multiwfn分析polar关键词输出的这个功能只支持Gaussian 09及之后版本,不支持更老版本。
Multiwfn的这个功能还支持计算与超瑞利散射(Hyper-Rayleigh Scattering, HRS)实验相关的各种量,在另一篇文章《使用Multiwfn计算与超瑞利散射(HRS)实验相关的量》(http://sobereva.com/499)当中做了详细介绍。
如果你使用了本文介绍的Multiwfn的功能,请在发表文章时提及研究中使用了Multiwfn提取Gaussian输出文件中的相关数据并计算了相关的量,并应当根据Multiwfn程序启动时提示的信息恰当引用Multiwfn程序。
2 Gaussian中(超)极化率的计算
这一节介绍在Gaussian中计算(超)极化率的基本原理和所需要的关键词。
将能量E对均匀外电场F进行Taylor展开得到如下式子
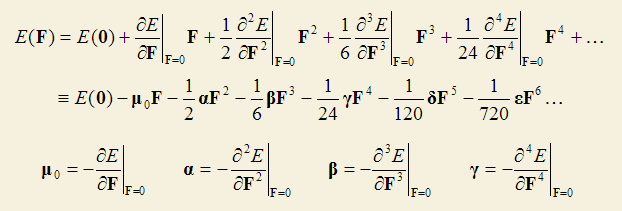
μ0就是分子的永久偶极矩矢量(无外场下的偶极矩)。α是分子的极化率,也称线性光学系数,是个3*3二阶张量。β是第一超极化率,也称分子的二阶非线性光学(NLO)系数,是个3*3*3的三阶张量。γ是第二超极化率,亦称分子的三阶NLO系数,研究得相对少一些。而更高的δ极少被讨论。(超)极化率数值和电场频率是相关的,外场频率为0的情况被称为静态(超)极化率;如果外场频率不是0,比如某一频率的光,对应的就是动态(超)极化率,或者叫含频(超)极化率。
Gaussian的polar关键词求这些量是通过导数方法,其原理很明确。如上式可见,求极化率要令能量对外场做两次导数,求第一超极化率要做三次导数。
求能量的导数分为三种情况:
(1)解析导数。这种方法求导数又快又精确,但是编程实现很困难,特别是对于高级的后HF而言。这种方式求能量导数时需要用到分子轨道系数对外场的导数,这通过求解CPHF方程来实现。并且利用含频CPHF方程,可以得到动态(超)极化率。这种求(超)极化率的方式也被称为CPHF方法。
(2)数值导数。这种方式通过有限差分方式得到能量的导数,也称为有限场(FF)方法。有限差分在所有数值算法书里都会介绍,比如求一个函数f在0处的导数可表示为f(0)=[f(0.001)-f(-0.001)]/(2*0.001)。通过这种方法求(超)极化率非常费时间,需要在不同数值、不同方向的外场下计算很多很多次单点,而且求高阶导数精度很差,因为每求一次数值导数都会由于数值噪音而累积误差,随着求导阶数增加误差迅速放大,做二阶以上导数时精度就很烂了(除非通过额外修正、外推等特殊方式处理)。另外,通过数值导数也没法求得动态(超)极化率。
(3) 解析+数值混合导数。这就是基于低阶解析导数,再通过一次或多次有限差分求高阶导数以获得(超)极化率的方法。精度和速度介于全解析导数和全数值导数之间。
Gaussian在支持解析导数方面已经算是很好的,对于HF、DFT、半经验方法都能支持到三阶解析导数,因此可以全解析地得到静态和含频的α和β(而其它量化程序都很难对HF/DFT/半经验支持到这么高阶导数,通常也就能支持到二阶)。对这类支持三阶解析导数的方法,使用polar关键词就会直接给出α和β的结果。如果同时写上CPHF=RdFreq,并且在输入文件末尾空一行写上外场频率w,比如0.05 0.12 0.3或532nm 670nm(静态的情况总是会被计算,故不需要特意写),就会计算含频极化率α(-ω;ω)和含频第一超极化率β(-ω;ω,0)。如果要算的含频第一超极化率是SHG形式,即β(-2ω;ω,ω),就写polar=DCSHG即可,此时CPHF=RdFreq可以忽略不写,并且此时β(-ω;ω,0)也会照样计算。
对于MP2等Gaussian只能支持到二阶解析导数的方法,可以全解析地计算α,但是若想计算β,就得再做一次有限差分才行。Gaussian中,此时直接写polar只会计算α,若还想得到β就得写polar=Cubic,会自动基于解析二阶导数做有限差分来得到三阶导数。
对于CISD、QCISD、CCSD、MP3、MP4(SDQ)等Gaussian只支持一阶解析导数的方法,直接写polar关键词会基于解析一阶导数做一次有限差分得到二阶导数,即α。若还想得到β就得写polar=DoubleNumer(等价于polar=enonly),会基于解析一阶导数做两次有限差分得到三阶导数。
对于CCSD(T)、QCISD(T)、MP4(SDTQ)、MP5等Gaussian只支持计算单点能的方法,写polar关键词会对能量做两次有限差分并由此得到α。对于它们在Gaussian里没有办法直接给出β。
注意对于HF、DFT、半经验以外的方法,Gaussian都没法给出含频(超)极化率。
若想得到更高阶导数计算更高阶超极化率,比如DFT下计算第二超极化率γ,需要基于其解析三阶导数做一次有限差分。从G09 D.01开始,对于支持三阶解析导数的方法可以用polar=gamma来算静态γ和动态的γ(-2ω;ω,ω,0)、γ(-ω;ω,0,0),会基于解析三阶导数自动做有限差分来得到所需的四阶导数。末尾应空一行写上外场频率。
值得一提的是,利用Multiwfn,可以通过完全态求和方法基于Gaussian的CIS/TDHF/TDDFT计算的输出得到静态或动态的极化率和第一、二、三超极化率,见《使用Multiwfn基于完全态求和(SOS)方法计算极化率和超极化率》(http://sobereva.com/232)。Multiwfn还能图形化展现(超)极化率,见《使用Multiwfn通过单位球面表示法图形化考察(超)极化率张量》(http://sobereva.com/547)。
3 使用Multiwfn解析polar关键词的输出
对于上一节讨论的各种情况,polar关键词输出的信息都能被Multiwfn所解析。注意route section一定要写上#P,否则输出文件将无法被正确解析。
启动Multiwfn后,先输入Gaussian的polar任务的输出文件的路径,比如C:\CH3NH2_polar.out,然后进入主功能24,选1,之后会看到下面的菜单:
-3 Set unit in the output, current: a.u.
-2 Set output destination, current: Output to screen
-1 Toggle loading frequency-dependent result for options 1 and 7, current: No
0 Return
1 "Polar" + analytic 3-order deriv. (HF,pure/hybrid DFT,semi-empirical)
2 "Polar" + analytic 2-order deriv. (MP2,double-hybrid DFT,TDDFT,CIS...)
3 "Polar=Cubic" + analytic 2-order deriv.
4 "Polar" + analytic 1-order deriv. (CISD,QCISD,CCSD,MP3,MP4(SDQ)...)
5 "Polar=DoubleNumer" or "Polar=EnOnly" + analytic 1-order deriv.
6 "Polar" + energy only (CCSD(T),QCISD(T),MP4(SDTQ),MP5...)
7 "Polar=gamma" + analytic 3-order deriv. (HF,DFT,semi-empirical)
选项1~7对应上一节提到的不同情况,当前你在什么情况下计算的就选哪种,然后Multiwfn就会输出分析的结果。比如你用了CCSD结合polar=doublenumer就应当选5。之所以要对此进行选择是因为不同情况下Gaussian的输出格式相差极大,Multiwfn必须知道你在什么情况下计算的,才能相应地对输出内容进行解析。选项1~7都可以给出α,只有1、3、5才会给出β,只有7才会给出γ。
如果在HF/DFT/半经验计算时用了polar CPHF=rdfreq或polar=DCSHG做了含频(超)极化率计算,或者用的是polar=gamma,默认情况下只会解析静态的(超)极化率。如果想让Multiwfn分析含频的,应当先选-1将其状态切换为Yes。当Gaussian输入文件里定义了多个频率时,如0.1,0.22,0.35,用户可以选择分析哪个频率下的结果。对于β,用户也可以选择分析β(-ω;ω,0)还是β(-2ω;ω,ω),注意只有写了DCSHG时选择β(-2ω;ω,ω)才有意义。对于γ,可以选择分析γ(-2ω;ω,ω,0)还是γ(-ω;ω,0,0)。
默认情况下输出的单位是a.u.,如果选-3,也可以切换为SI或esu单位。默认情况下输出信息会显示到屏幕上,也可以选-2来更改为输出到当前目录下的polar.txt当中。
如果你使用的是DFT或MP2,且对当前体系又要做振动分析又要算极化率,那么没必要分别做freq和polar任务,只要做一次freq即可。用Multiwfn载入freq任务的输出文件,在Multiwfn此文介绍的界面里选择2 "Polar" + analytic 2-order deriv.即可提取极化率。
3.1 解析静态极化率和第一超极化率一例
下面就以分析甲胺在#P PBE1PBE/aug-cc-pVTZ polar关键词下得到的输出文件为例进行说明。
当前例子用的是PBE1PBE,是DFT中常用的一种泛函,故对应的是前述第一种情况,因此当我们看到上面的菜单时应选1,然后马上会看到α和β的分析结果,下面将对各项的含义进行说明。我们先看α部分
Dipole moment:
X,Y,Z= -0.506266 0.150290 0.000000 Norm= 0.528103
Static polarizability:
XX= 25.04620
XY= -0.08830
YY= 28.89110
XZ= 0.00000
YZ= 0.00000
ZZ= 24.43580
Isotropic average polarizability: 26.12437
Isotropic average polarizability volume: 3.871231 Angstrom^3
Polarizability anisotropy (definition 1): 4.18643
Polarizability anisotropy (definition 2): 4.18363
Eigenvalues of polarizability tensor: 24.4358 25.0442 28.8931
Polarizability anisotropy (definition 3): 4.15314
如前所述,默认情况下所有输出的量都是以a.u.为单位。
极化率张量是个对称的3*3矩阵,故所以只有6个独立的矩阵元列了出来。每个体系的极化率的大小一般只用一个数值<α>来表示,也就是上面给出各向同性平均极化率,它是对XX、YY、ZZ取平均得到的。极化率也经常通过极化率体积来表示,上面也给出了。极化率并不是各向同性的,体系对不同方向射来的电场的响应是不同的。如上可见,Multiwfn也输出了极化率的各向异性值Δα,数值越大各向异性越强,球对称体系显然其值为0。各向异性可以以三种方式定义,分别如下所示,详见Multiwfn手册3.27.1节
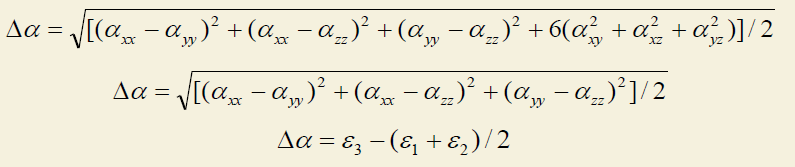
ε代表极化率张量的本征值,它也被Multiwfn输出了出来。最常见的衡量极化率的各向异性程度是定义2,而定义3的形式一般是在衡量磁屏蔽张量各向异性时用的。
下面是第一超极化率部分的解析结果
Static first hyperpolarizability:
XXX= 13.173100
XXY= 4.937890
XYY= 13.647700
YYY= -35.484000
XXZ= 0.000000
XYZ= 0.000000
YYZ= 0.000000
XZZ= -2.763570
YZZ= 1.342190
ZZZ= 0.000000
Beta_X= 24.05723 Beta_Y= -29.20392 Beta_Z= 0.00000
Magnitude of first hyperpolarizability: 37.836745
Projection of beta on dipole moment: -31.373491
Beta || : -18.824094
Beta ||(z) : 0.000000
Beta _|_(z) : 0.000000
Gaussian的β的输出有个众所周知的问题,也就是符号是反的,即每个β元素的数值都应该乘以-1,至少直到G09 D.01版依然存在这个问题。有文章专门指出了这点,见《Gaussian程序计算的一阶超极化率的符号问题》(四川师范大学学报(自然科学版),33,228)。这个问题在Multiwfn中已经被考虑进去了,Multiwfn输出的β的符号都是正确的。
β有3*3*3=27个元素。静态β满足Kleinman对称性,三个标号可以随意置换而完全不影响结果,比如xyy=yxy=yyx,只有10个元素是唯一的,所以Multiwfn也只输出了10个元素。
Beta_X、Beta_Y、Beta_Z衡量的是β在X、Y、Z方向上的分量。Magnitude of first hyperpolarizability体现了β的整体的大小。其定义分别如下所示
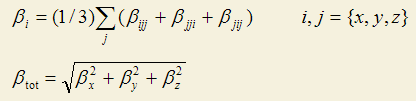
只有β在偶极矩方向上的投影值才是可以通过电场诱导二次谐波产生实验(EFISH)测量出来的,和实验值对比通常比的都是这个值。Multiwfn给出了β在偶极矩方向上的投影值(β_prj,一些文中也写为β_vec)。另一个文献中常见的量是Beta ||,||代表平行于偶极矩,它正比于β_prj
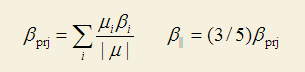
文献中常见的Beta ||(z)和Beta _|_(z)的定义如下所示,分别衡量的是平行和垂直于Z方向上的β的值
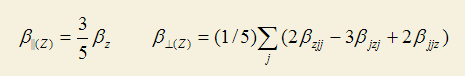
当偶极矩方向和Z方向一致时,Beta_Z=β_prj,Beta ||(z)=Beta ||。
值得一提的是,默认情况下,Gaussian会将输入文件里体系的坐标调整到标准朝向下,这通常会令体系发生旋转。Gaussian计算出的,也即Multiwfn所解析的,都是标准朝向下的结果,因此X、Y、Z可能和你的输入文件里的笛卡尔轴方向不对应。如果想避免自动调整到标准朝向,用nosymm关键词。
3.2 解析动态极化率和第一超极化率一例
此例使用Multiwfn解析polar关键词产生的动态(超)极化率。输入文件如下,分别计算外场为0.07和0.1 a.u.的情况。
#p PBE1PBE/aug-cc-pVTZ polar CPHF=RdFreq
test
0 1
C -0.55391731 0.43227932 0.14513431
H -1.29461381 -0.13844703 0.71478821
H -0.40071988 1.37810560 0.67504812
H -0.99858078 0.66864399 -0.83680924
N 0.70741247 -0.31205725 0.11165308
H 0.57479710 -1.18908235 -0.38659422
H 1.39864521 0.20863272 -0.42322026
0.07 0.1
令Multiwfn载入输出文件,并进入主功能24里的子功能1后,先选-1切换成解析动态值,然后再选1。然后程序问载入哪个频率下的结果,此例我们选2,即w=0.07的情况。然后我们得到了w=0.07下的极化率输出。之后程序问分析β(-ω;ω,0)还是β(-2ω;ω,ω)的结果。由于没写DCSHG,我们只能选择β(-ω;ω,0)。输出如下
Frequency-dependent first hyperpolarizability Beta(-w;w,0)
XXX= 16.334900
XYX= YXX= 7.369050
YYX= 16.593300
XZX= ZXX= 0.000000
YZX= ZYX= 0.000000
ZZX= -2.918320
XXY= 8.947060
XYY= YXY= 15.473800
YYY= -40.341800
XZY= ZXY= 0.000000
YZY= ZYY= 0.000000
ZZY= 1.240500
XXZ= 0.000000
XYZ= YXZ= 0.000000
YYZ= 0.000000
XZZ= ZXZ= -2.796870
YZZ= ZYZ= 1.609830
ZZZ= 0.000000
Beta_X= 29.34451 Beta_Y= -30.96003 Beta_Z= 0.00000
Magnitude of first hyperpolarizability: 42.657048
Projection of beta on dipole moment: -36.941911
Beta || : -22.165146
Beta ||(z) : 0.000000
Beta _|_(z) : 0.000000
和上一例相比,可见在含频外场下β值增大了。各项的含义和上例一致,不再累述。值得一提的是对于beta(-ω;ω,0)这种情况,只有i,j,k三个标号中的i,j可以互换,比如xyy=yxy≠yyx,张量的对称性没有静态β的那么高,故有18个独立的元素。不过,当外场频率不是很大时,Kleinman对称性是可以近似满足的,从上面的结果可见,诸如xyx和xxy相差不算很大。
假设我们要看w=0.1时的β(-ω;ω,0),那么再次进入此功能,然后选1-3-1即可。
基于当前输出文件没法查看β(-2ω;ω,ω),因为当前例子没写DCSHG。要看它的话应把polar后面加上=DCSHG重算一次,然后再进入此功能,并选择分析β(-2ω;ω,ω)情况的数据。
3.3 解析第二超极化率一例
这里我们对NH3计算第二超极化率γ。Gaussian输入文件是Multiwfn程序包里的examples\polar\NH3_gamma.gjf,内容如下
#p PBE1PBE/daug-cc-pVTZ polar=gamma
[空行]
pbe1pbe/aug-cc-pVTZ opted
[空行]
0 1
N 0.00000000 0.00000000 0.11367600
H 0.00000000 0.93902800 -0.26524400
H -0.81322200 -0.46951400 -0.26524400
H 0.81322200 -0.46951400 -0.26524400
[空行]
532nm 680nm
想高精度计算小体系的γ,基组必须带非常充足的弥散函数,因此此例用了每个角动量加两层弥散的d-aug-cc-pVTZ,此基组非常昂贵。另外计算γ本身也很昂贵,所以哪怕是小体系,想高精度计算γ也需要给力的机子。polar=gamma关键词要求既计算静态的也计算动态的γ,如当前输入文件所示,对于动态的γ我们要计算的是532 nm和680 nm外场下的情况。
此例我们要解析γ(-2w;w,w,0)在680 nm下的结果。启动Multiwfn然后输入
examples\polar\NH3_gamma.out
24 //(超)极化率分析
1 //解析Gaussian的(超)极化率的计算输出
-1 //切换为载入动态(超)极化率(不选这个的话之后解析的将是静态的γ)
7 //对应polar=gamma的情况
2 //对应680 nm的情况
2 //解析γ(-2w;w,w,0)形式的动态第二超极化率
输出信息如下
XXXX= 3091.740000
YXXX= 0.000000
ZXXX= 0.000040
XYXX=XXYX= 0.000000
...略
YZYZ=YYZZ= 3677.510000
ZZYZ=ZYZZ= -0.446631
XZZZ= 0.000000
YZZZ= -0.400105
ZZZZ= 18072.400000
Magnitude of gamma: 5998.270291
X component of gamma: 1574.323333
Y component of gamma: 1574.284000
Z component of gamma: 5569.774000
Average of gamma (definition 1), gamma ||: 8718.3813
Average of gamma (definition 2): 8737.028000
gamma _|_: 2875.049333
上面每一项的定义笔者就不在这里介绍了,因为在Multiwfn手册3.27.1节里已经写得非常详细了,这些量都是考察γ时经常要涉及的。
如屏幕上的提示所示,上面给出的gamma信息对应的是输入朝向下的,而之前提到的Multiwfn给出的alpha和beta都是标准朝向下的,这个差异要注意。