过渡态、反应路径的计算方法及相关问题

前言：本文主要介绍过渡态、反应路径的计算方法，并讨论相关问题。由于这类算法极多，可以互相组合，限于精力不可能面面俱到展开，所以只介绍常用，或者实用价值有限但有启发性的方法。文中图片来自相关文献，做了一定修改。由于本文作为帖子发布，文中无法插入复杂公式，故文中尽量将公式转化为文字描述并加以解释，这样必然不如公式形式严谨，而且过于复杂的公式只能略过，但我想这样做的好处是更易把握方法的梗概，有兴趣可以进一步阅读原文了解细节。虽然绝大多数人不专门研究计算方法，其中很多方法也不会用到，但多了解一下对开阔思路是很有好处的。笔者后来还写了《简谈Gaussian里找过渡态的关键词opt=TS和QST2、3》（http://sobereva.com/460）一文，专门针对Gaussian里找过渡态的关键词的具体使用问题进行了说明，建议Gaussian用户都看看。

文中指的“反应”包括构象变化、异构化等任何涉及到过渡态的变化过程。“反应物”与“产物”泛指这些过程的初态和末态。“优化”若未注明，包括优化至极小点和优化至过渡态。势能面是高维的，但为了直观以及表述方便，文中一般用二维势能面模型来讨论，应推广至高维情况。限于纯文本格式，向量、矩阵无法加粗表示，但容易自行判断。

如果想了解更多的关于优化、找过渡态、产生IRC算法的细节以及数学方面的东西，参看“几何优化、过渡态搜索、IRC综述与原文合集”（http://bbs.keinsci.com/thread-105-1-1.html）。

目录：

1.过渡态
2.过渡态搜索算法
 2.1 基于初猜结构的算法
  2.1.1 牛顿-拉弗森法(Newton-Raphson,NR)与准牛顿法(quasi-Newton,QN)
  2.1.2 AH方法(augmented Hessian)
   2.1.2.1 RFO法(Rational Function Optimization，有理函数优化)
   2.1.2.2 P-RFO法(Partitioned-RFO)
   2.1.2.3 QA法(Quadratic Approximation，二次逼近)
   2.1.2.4 TRIM法(trust-region image minimization，置信区域镜像最小化)
   2.1.2.5 在高斯中的常见问题
  2.1.3 GDIIS法(Geometry Direct Inversion in the Iterative Subspace)
  2.1.4 梯度模优化(gradient norm minimization)
  2.1.5 Dimer方法
 2.2 基于反应物与产物结构的算法
  2.2.1 同步转变方法(synchronous transit,ST)
  2.2.2 STQN方法(Combined Synchronous Transit and Quasi-Newton Methods)
  2.2.3 赝坐标法(pseudo reaction coordinate)
  2.2.4 DHS方法(Dewar-Healy-Stewart，亦称Saddle方法)与LTP方法(Line-Then-Plane)
  2.2.5 Ridge方法
  2.2.6 Step-and-Slide方法
  2.2.7 Müller-Brown方法
  2.2.8 CI-NEB、ANEBA方法
 2.3 基于反应物结构的算法
  2.3.1 最缓上升法(least steep ascent,shallowest ascent)
  2.3.2 本征向量/本征值跟踪法(eigenvector/eigenvalue following,EF。也称mode walking/mode following/Walking up valleys)
  2.3.3 ARTn(activation-relaxation technique nouveau)
  2.3.4 梯度极值法(Gradient extremal,GE)
  2.3.5 约化梯度跟踪(reduced gradient following,RGF)
  2.3.6 等势面搜索法(Isopotenial Searching)
  2.3.7 球形优化(Sphere optimization)
 2.4 全势能面扫描
3.过渡态相关问题
 3.1 无过渡态的反应途径(barrierless reaction pathways)
 3.2 Hammond-Leffler假设
 3.2 对称性问题
 3.3 溶剂效应
 3.4 计算过渡态的建议流程
4.内禀反应坐标(intrinsic reaction coordinate,IRC)
5.IRC算法
 5.1 最陡下降法(Steepest descent)
 5.2 IMK方法(Ishida-Morokuma-Komornicki)
 5.3 Müller-Brown方法
 5.4 GS(Gonzalez-Schlegel)方法
6.chain-of-states方法
 6.1 Drag method方法
 6.2 PEB方法(plain elastic band)
 6.3 Elber-Karplus方法
 6.4 SPW方法(Self-Penalty Walk)
 6.5 LUP方法(Locally Updated planes)
 6.6 NEB方法(Nudged Elastic Band)
 6.7 DNEB方法(Double Nudged Elastic Band)
 6.8 String方法
 6.9 Simplified String方法
 6.10 寻找过渡态的chain-of-state方法
  6.10.1 CI-NEB方法
  6.10.2 ANEBA方法(adaptive nudged elastic band approach)
 6.11 chain-of-states方法的一些特点
 6.12 高斯中opt关键字的path=M方法
 6.13 CPK方法(Conjugate Peak Refinement)

1.过渡态

本质上，电子、原子核的运动是相关而不可分割的，求解薛定谔方程得到的是描述二者状态的总波函数和体系的总能量。在量子化学中，为简化问题，一般采用BO(Born-Oppenheimer)近似。由于电子比原子核轻得多，其运动速度远快于原子核，核坐标改变过程中的每一时刻电子的状态可以立即调整以使能量最低，而以电子的视角看原子核就是不动的势场，所以有理由将原子核运动与电子的运动分离开来。可以在每一组确定的核坐标情况下求解电子的薛定谔方程，电子能量加上核间互斥能即得到此几何结构下的分子总能量。这种BO近似的做法由于在求解电子薛定谔方程时忽略了核运动，所以也称为核不动近似。在BO近似下分子的能量是核坐标的函数，系统地变化核坐标，随之变化的能量就构成了势能面(potential energy surface,PES)。

过渡态结构指的是势能面上反应路径上的能量最高点，它通过最小能量路径(minimum energy path,MEP)连接着反应物和产物的结构（如果是多步反应的机理，则这里所指反应物或产物包括中间体）。对于多分子之间的反应，更确切来讲过渡态结构连接的是它们由无穷远接近后因为范德华力和静电力形成的复合物结构，以及反应完毕但尚未无限远离时的复合物结构。确定过渡态有助于了解反应机理，以及通过势垒高度计算反应速率。一般来讲，势垒小于21kcal/mol就可以在室温下发生。

在势能面上，过渡态结构的能量对坐标的一阶导数为0，只有在反应坐标方向上曲率（对坐标二阶导数）为负，而其它方向上皆为正，是能量面上的一阶鞍点。过渡态结构的能量二阶导数矩阵（Hessian矩阵）的本征值仅有一个负值，这个负值也就是过渡态拥有唯一虚频的来源。若将分子振动简化成谐振子模型，这个负值便是频率公式中的力常数，开根号后即得虚数。

分子构象转变、化学反应过程中往往都有过渡态的存在，即这个过程在势能面上的运动往往都会经历满足上述条件的一点。化学反应的过渡态更确切应当成为“反应过渡态”。需要注意的是化学反应未必都经历过渡态结构。

由于过渡态结构存在时间极短，所以很难通过实验方法获得，直到飞秒脉冲激光光谱的出现才使检验反应机理为可能。计算化学方法在目前是预测过渡态的最有力武器，尽管计算上仍有一些困难，比如其附近势能面相对于平衡结构更为平坦得多、低水平方法难以准确描述、难以预测过渡态结构、缺乏绝对可靠的方法（如优化到能量极小点可用的最陡下降法）等。

搜索过渡态的算法一般结合从头算、DFT方法，在半经验、或者小基组条件下，难以像描述平衡结构一样正确描述过渡态结构，使得计算尺度受到了限制。结合分子力场可以描述构象变化的过渡态，但不适用描述反应过渡态，因为大部分分子力场的势函数不允许分子拓扑结构的改变，虽然也有一些力场如ReaxFF可以支持，有的力场还有对应的过渡态原子类型，但目前来看适用面仍然较窄，而且不够精确，尽管更为快速。

注：严格来说，“过渡结构”是指势能面上反应路径上的能量最高点，而“过渡态”是指自由能面上反应路径上的能量最高点，由于自由能变主要贡献自势能部分，所以多数情况二者结构近似一致。为了计算上的简单，常以势能面近似表达自由能面，以下述方法得到的势能面上反应路径上的能量最高点做为过渡态。但随着温度升高，往往熵变的贡献导致自由能面与势能面形状发生明显偏离，从而导致过渡结构与过渡态明显偏离，两个词就不能混用了，此时下述方法应该用在自由能面上找真正的过渡态。但本文不涉及相关问题，故文中过渡态、过渡结构一律指势能面上反应路径上的能量最高点。

2.过渡态搜索算法

2.1 基于初猜结构的算法

2.1.1 牛顿-拉弗森法(Newton-Raphson,NR)与准牛顿法(quasi-Newton,QN)

NR法是寻找函数一阶导数为0（驻点）位置的方法。通过对能量函数的泰勒级数的二阶近似展开，然后使用稳态条件dE/dr=0，可导出步进公式：下一步的坐标向量 = 当前坐标向量 - 能量一阶导数向量 * Hessian矩阵的逆矩阵。在势能面上以NR法最终找到的结果是与初猜位置Hessian矩阵本征值正负号一致、离初猜结构最近的驻点，由于能量极小点、过渡态和高阶鞍点的能量一阶导数皆为0，故都可以用NR法寻找。

对于纯二次形函数NR法仅需一步即可找到正确位置，而势能面远比之复杂，所以需要反复走步直至收敛。也因为势能面这个特点，为了改进优化，实际应用中NR法一般还结合线搜索步(line search)，对于优化至极小点，就是找当前点与NR法算出来的下一点的连线上的能量极小点作为实际下一步结构；若优化至过渡态，且连线方向主要指向过渡态，则找的是连线上能量极大点，若主要指向其它方向则找连线的能量极小点，若指向二者程度均等则一般不做线搜索。由于精确的线搜索很花时间，所以一般只是在连线的当前位置附近计算几个点的能量，以高阶多项式拟和后取其最小/最大点。

NR法每一步需要计算Hessian矩阵并且求其逆，所以十分昂贵。QN法与NR法的走步原理一样，但Hessian矩阵最初是用低级或经验方法猜出来的，每一步优化中通过当前及前一步的梯度和坐标对Hessian矩阵逆矩阵逐渐修正。由于只需计算一阶导数，即便Hessian矩阵不准确造成所需收敛步数增加，但一般仍比NR法速度快得多。QN法泛指基于此原理的一类方法，常用的是BFGS(Broyden Fletcher Goldfarb Shanno)，此法对Hessian的修正保持其对称性和正定性，最适合几何优化，但显然不能用于找过渡态。还有DFP(Davidon-Fletcher-Powell)，MS(Murtagh-Sargent，亦称symmetric rank 1，SR1)，PSB(Powell-symmetric-Broyden)。也有混合方法，如Bofill法是PSB和MS法对Hessian修正量的权重线性组合，比二者独立使用时更好，权重系数通过位移、梯度改变量和当前Hessian计算得到，它对Hessian的修正不强制正定，很适宜搜索过渡态。

将NR步进公式放到Hessian本征向量为坐标的空间下其意义更为明显（此时Hessian为对角矩阵），可看出在每个方向上的位移就是这个方向势能的负梯度除以对应的本征值，比如在i方向上的位移可写为ΔX(i)=-g(i)/h(i)，在受力越大、曲率越小的方向位移越大。每一步实际位移就是这些方向上位移的矢量和。对于寻找过渡态，因为虚频方向对应Hessian本征值为负，使位移为受力相反方向，所以NR法在过渡态附近每一步都是使虚频方向能量升高，而在其它正交的方向朝着能量降低的方向位移，通过这个原理步进到过渡态。若有n个虚频，则NR法就在n个方向升高能量而其它方向降低能量找到n阶鞍点。

由于NR法的这个特点，为找到正确类型的驻点，初猜结构必须在目标结构的二次区域(quadratic region)内。所谓的二次区域，是指驻点附近保持Hessian矩阵本征值符号不变的区域，它的形状可以用多变量的二次函数准确描述，例如二维势能面情况下这样的区域可以用F(x,y)=A*x^2+B*y^2+C*x+D*y+E*x*y来近似描述。对于能量极小点，就是指初猜点在目标结构附近Hessian矩阵为正定矩阵的范围；对于找过渡态，就需要初猜点在它附近含有且仅含有一个负本征值的范围内。并且这个范围内不能有其它同类驻点比目标结构距离初猜结构更近。NR法方便之处是只需要提供一个初猜结构即可，但是由于过渡态二次区域很小（相对于能量极小点来讲），复杂反应过渡态又不容易估计，故对使用者的直觉和经验有一定要求，即便是老手，也往往需要反复尝试。

NR法对初猜结构比较敏感，离过渡态越近所需收敛步数越少，成功机率越高。模版法可以帮助给出合理的初猜，也就是如果已经知道其它机理相同的反应的过渡态结构，可以保持反应位点部分的结构不变而替换周围的原子，使之变成自己要研究的化合物反应的初猜结构。

2.1.2 AH方法(Augmented Hessian)

AH方法并不是独立的寻找过渡态的方法，而是通过修改原始Hessian矩阵来调整NR法步进的长度和方向的一种方法。在NR法的步进公式中加入了一个移位参数λ，式子变为ΔX(i,λ)=-g(i)/(h(i)-λ)，NR法相当于λ等于0时的特例。λ控制着每步步进距离，它与h(i)的相对大小也控制着这个坐标上的步进方向。根据设定λ方法的不同，常见的有RFO、P-RFO和QA/TRIM。这些方法每一步也使用QN方法来快速地更新Hessian。

下面提及的置信半径R(Trust radius)是指二阶泰勒级数展开这种近似的合理的区域，可以在优化过程中固定也可以动态改变，比如下一步位置的实际能量与使用二阶泰勒级数展开预测的能量符合较好则加大R，反之减小。优化的每一步移动距离不应超过R，否则可能进入二阶泰勒级数展开近似的失效区域，NR法在势能面平坦的时候容易超过这个范围，应调整λ避免。

2.1.2.1 RFO法(Rational Function Optimization，有理函数优化)

与NR法不同的是，RFO对能量函数使用的是有理逼近展开，从形式上讲就是将NR法的二阶泰勒级数展开式作为分子，多添加了个分母项，可推得它与AH方法有形式相同的步进公式。确定其中λ的公式是λ=∑( g(i)^2/(h(i)-λ) )，g(i)和h(i)代表此方向的梯度和本征值，加和是对所有本征向量方向加和。通过迭代方法会解出N+1个λ（N代表势能面维数），将λ按大小排列，则有λ(i)≤h(i)≤λ(i+1)。故选其中最小的λ可使各个方向位移公式的(h(i)-λ)项皆为正，保证每步位移都向着极小点。选其中大于m个Hessian本征值的λ，将会在本征值最低的m个方向上沿其上的受力反方向位移提升能量，在其余N-m个方向上降低能量，由此确保优化到m阶鞍点，若m为1即用来找过渡态。所以用了这个方法寻找指定类型驻点不再像NR法对初猜位置Hessian本征值符号有要求，而是直接通过选择λ来设定向着何种鞍点位移。如果每步步长度超过了R，则乘以一个小于1的因子来减小步长。值得一提的是，λ与势能面维数N的平方根近似成正比，随着体系尺度的增大，RFO的λ对NR法的二次近似就会趋现“校正过度”情况，产生大小不一致问题，可使用SIRFO(Size independent RFO)方法解决，即AH走步公式中的λ改为λ/N^0.5。

2.1.2.2 P-RFO法(Partitioned-RFO)

P-RFO法专用于优化过渡态，效率比RFO更高。RFO对所有方向的步进都使用同一个λ，而在P-RFO中在指向过渡态的方向使用独立计算的λ(TS)，λ(TS)=g(TS)^2/(h(TS)-λ(TS))，应选这个一元二次方程的最大的解，可保证在这个方向上升高能量。其余方向λ的确定和RFO的公式一样，加和就不再包含指向过渡态的方向，并且选最小的λ解以使这些方向能量降低。这里所谓指向过渡态的方向一般是指最低本征值的方向，在上述RFO方法m为1时也是如此假设（限于其形式RFO也只能用这最低模式），但有时会是其它的非最低的模式，P-RFO也可以将这样的模式作为指向过渡态的模式，见后文EF方法的讨论。

2.1.2.3 QA法(Quadratic Approximation，二次逼近)

确定λ的公式是(ΔX(i))^2=∑( -g(i)/(h(i)-λ) )^2=R^2，也就是说每一步移动的距离恰好是置信半径，这样步进速度较快。若优化到过渡态，计算λ公式的加和中指向过渡态本征向量的那一项的λ改为-λ，即ΔX(TS)=-g(TS)/(h(TS)+λ)。

2.1.2.4 TRIM法(trust-region image minimization，置信区域镜像最小化)

这个方法假设Hessian本征值最小的方向的梯度和曲率符号与原本相反，而其它方向不变。经过这样的变化后原来的过渡态位置就成为了能量极小点(过渡态的image)，这样就可以通过优化到极小点而得到过渡态。将TRIM的假设g(TS)'=-g(TS)，h(TS)'=-h(TS)代入AH方法的步进公式ΔX(i,λ)=-g(i)/(h(i)-λ)，再使分子分母同乘以-1，可知在过渡态方向上的步进公式与其它方向区别仅在于反转了λ的符号。又由于TRIM也是通过调整λ使步进长度等于为置信半径，所以在公式的形式上与QA法找过渡态的公式完全一致，QA与TRIM可互为同义词。

通过如上调整AH方法引入的λ可使NR法的步进更有效率、更稳定，还可以通过它改变步进公式在不同方向上的分母项符号，使优化过渡态的初猜点不限于过渡态的二次区域。可直接指定沿某个振动模式升高能量来找过渡态，即便当前点这个方向的Hessian本征值可能是正值，例如从极小点开始跟踪至过渡态，见后文的EF方法。

2.1.2.5 在高斯中的常见问题

高斯中opt=ts是使用Berny算法来找过渡态，需要提供一个初猜结构。Berny默认的走步的方法是RFO/P-RFO(分别对于优化至极小值/鞍点），若加了Newton选项，则走步基于NR法。每一步对Hessian矩阵的更新方法以UpdateMethod选项指定，寻找极小点时默认用BFGS，找过渡态时默认用Bofill。Berny算法还包括一些细节步骤在内，比如投影掉被冻结的变量、更新置信半径、设定了线搜索过程中几种方案等等，详见手册opt关键字。

使用了每步修正Hessian的准牛顿法后，初猜的Hessian矩阵质量明显影响结构收敛速度，它的不准确容易导致搜索过渡态失败（在高斯中默认使用价力场得到Hessian）。这种情况需要昂贵的calcfc关键字以当前方法水平计算最初的Hessian矩阵，若使用的方法在程序中支持解析二阶导数，速度会较好。或者用readfc来读取包含了Hessian矩阵信息的chk文件，可以先使用低水平方法进行简正振动分析得到chk文件，再将之读入作为Hessian矩阵初猜，能够节约时间，但前提是此势能面对方法等级不敏感（一般如此）。使用了更准确的初猜后不仅可以增加找到过渡态的成功机率，还有助于在更短的优化步数内达到收敛标准。若使用calcall，则每一点都重新准确计算Hession，会更为可靠，但极为昂贵。

高斯中berny方法寻找过渡态默认每步会检查Hessian矩阵的本征值是否仅有一个为负，如果不符，就会提示“a wrong sign eigenvalue in hessian matrix”，经常一开始就报错，原因是初猜结构不符合这个条件，即便这个初猜通过berny方法最终能够正确优化到过渡态，这时应加noeigentest选项避免本征值符号的检查，不符合要求也继续优化，但有一定可能收敛到其它类型驻点。

高斯中默认的置信半径为0.3 bohr，若优化中步长（RFO/P-RFO步）超过就会输出“Maximum step size (   0.300) exceeded in Quadratic search”和“Step size scaled by xxx”，即乘以xxx调小步长至置信半径内。还有一种考虑更周到的调节方法是在置信半径代表的球面上优化寻找最佳的位置，这对向极小点优化是默认的，但对于寻找过渡态的优化时需要用nonrscale关键字打开。另外可以使用iop(1/8=k)或等价的maxstep=k将置信半径改为k*0.01 bohr(1 bohr=0.5292埃)，调大后往往可以显著减少收敛步数，很适合势能面平坦的大体系。注意并不是每一步的步长都固定为k*0.01 bohr，若没超过置信半径则步长并不因此改变。寻找极小点时默认为允许动态改变置信半径，此时iop(1/8)设的就是最初的置信半径，对于寻找过渡态默认为关闭此功能（相当于用了NoTrustUpdate），可以使用trustupdate关键字来打开这个功能。

2.1.3 GDIIS法(Geometry Direct Inversion in the Iterative Subspace)

GDIIS与DIIS原理一致，但用途不同，DIIS优化的是MO组合系数，GDIIS优化的是坐标变量。GDIIS方法趋于收敛到离初始位置最近的驻点，包括过渡态位置。下一步坐标X(new)=X"-H'g"，H'代表当前步的Hessian逆矩阵，可见公式形式与NR法是一致的，但是X"与g"不再指当前步的坐标和梯度，而是由之前走过的点的坐标X(k)和梯度g(k)插值得到的，X"=∑c(k)X(k)，g"=∑c(k)g(k)，代入上式即X(new)=∑c(i)(X(i)-H'g(i))，其中∑是对之前全部走过的点加和。系数c(k)通过使误差向量r的模最小化得到，r=∑c(k)e(k)，并以∑c(k)=1为限制条件。e(k)常见有两种定义，一种是e(k)=-H'g(k)，另一种更常用，是e(k)=g(k)，可看出GDIIS利用的是已经搜索过的子空间中坐标与梯度的相关性，通过外推方法估出梯度（即误差向量）的模尽可能小的坐标，这一点与后述的梯度模方法相似。

此方法缺点是由于势能面复杂，步进中容易被拉到已经过的势能面的其它驻点而不能到达指定类型驻点，还容易走到类似肩膀形状的拐点，梯度虽小却不为0，由于不能达到收敛标准而反复在此处震荡。另外随优化步数增加，误差向量数目逐渐加大，会逐渐出现的误差向量之间的线性相关，导致伪收敛和数值不稳定问题。在改进的方法中将GDIIS与更可靠的RFO方法结合，比较二者的步进方向和长度，并检验GDIIS中的组合系数c，根据一定规则来决定每一步对之前走过的点的保留方式，必要时全部舍去而重新开始GDIIS。Gaussian中用的这种改进的GDIIS方法解决了上述问题同时提高了效率，速度等于或优于RFO方法，尤其是以低水平对势能面平坦的大体系优化时更为突出。GDIIS计算量小，对Hessian矩阵很不敏感，可以在优化中不更新，也可以用QN法更新来改善性能。此方法自Gaussian98起就是默认的半经验方法的优化算法，其它方法下也可以用OPT(ts,gdiis)关键词，此时就不再用berny方法而是用GDIIS方法找过渡态。

2.1.4 梯度模优化(gradient norm minimization)

势能面上的驻点，包括能量极小点、过渡态和高阶鞍点的势能梯度都为0，所以在相应于势能面的梯度模面上进行优化找到数值为0的点，经过Hessian矩阵本征值符号的检验，就能得到过渡态。这相当于把搜索过渡态问题转化为了能量极小化问题，就有了更可靠的算法可用。（注：梯度模指的是势能梯度在各个维度分量平方和的平方根，即梯度大小的绝对值）。但是寻找数值更小点的优化方法比如最陡下降法只能找到离初始位置最近的极小点，若找到的梯度模面上的极小点数值大于0则是势能面肩膀形拐点，没有什么用处，而这样的点收敛半径往往很大，例如图中在x=2至8的区域内都会收敛到函数拐点，只有提供的初猜结构在x=1和9附近很小的范围内才会收敛到过渡态，收敛半径太小，难以提供合理初猜。梯度模面上还多出一些极大点，如x=1.5处，若使用收敛更快的NR法找极小点还容易收敛到这样没有意义的点上。基于这些原因，梯度模法很少使用。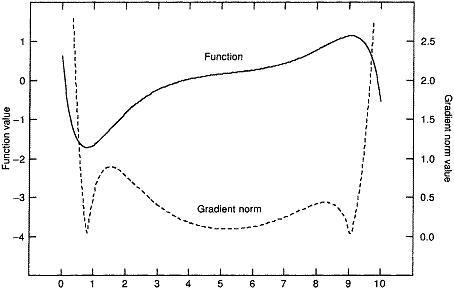

[图1]原函数与它的梯度模曲线

2.1.5 Dimer方法

Dimer方法是一种高效的定位过渡态的方法。这个方法定义了由两个点R1和R2组成的一个Dimer，能量和所受势能力（由原始的势能面梯度造成受力，下同）分别为E1和E2、F1和F2。两个点间距为2ΔR，ΔR为定值。这两点的中间点为R，其受力F(R)=(F1+F2)/2。Dimer的总能量为E=(E1+E2)/2。这个方法的每一步包括平移Dimer和旋转Dimer两步。

旋转Dimer：保持R1、R2中点位置R不变作为轴，旋转Dimer直到总能量E最小。通过推导可知在旋转过程中，E与R点在dimer方向（R1-R2方向）上的曲率关系C是线性的，即最小化E的过程就是最小化C的过程。所以每一步的Dimer方向都是曲率最小方向，当最终R收敛到过渡态位置时，Dimer就会平行于虚频方向。

平移Dimer：Dimer根据受力F'移动R的位置，结合不同方法有具体步进方式，如quick-win、共轭梯度法。当C<0（过渡态或高阶鞍点的二次区域内），F'等于将F(R)平行于Dimer方向力的分量符号反转；当C>0（极小点二次区域内），F'等于F(R)平行于Dimer方向力的分量的负值，而没有垂直于Dimer方向的力，促使Dimer尽快离开这个区域。由于Dimer的方向就是曲率最小的方向，在过渡态二次区域内就是指虚频方向，在Dimer方法中F'的定义使这个方向以受力相反方向移动以升高能量，而其它方向顺着受力方向移动来最小化能量，可看出原理上与NR法相似。费时的计算Hessian矩阵最小本征值以确定提升能量方向的过程被旋转Dimer这一步代替了，仅需要计算一阶导数。Dimer法对初始位置要求很宽松，并不需要在过渡态二次区域内，若在极小点二次区域内就类似于后述的EF方法沿着最小振动模式爬坡。如果在高阶鞍点二次区域内，只在曲率最负的虚频方向沿着受力反向移动，在其它虚频方向上仍最小化能量，而不会像NR法收敛到高阶鞍点。

[图2]右侧为Dimer法在Müller-Brown模型势上面搜索两个过渡态过程中Dimer走的路径

势能面上往往有许多鞍点，Dimer方法还可以做鞍点搜索。通过分子动力学方法给予Dimer一定动能，使之能够在势能面上广阔的区域内运动，根据一定标准提取轨迹中的一些点作为初猜，再执行标准Dimer方法就可以得到许多不同的鞍点。Dimer方法很适合双处理器并行，两个点的受力分别由两个处理器负责，速度可增加将近一倍。

2.2基于反应物与产物结构的算法

2.2.1 同步转变方法(synchronous transit,ST)

提供合理的初猜结构往往不易，ST方法可以只根据反应物和产物结构自动得到过渡态结构。“同步转变”这个名字强调的是反应路径上所有坐标一起变化，这是相对于后面提到的赝坐标法来说的（即只变化指定的坐标，尽管其它坐标优化后坐标也会变化）。

ST分为两种模型，最简单的就是LST模型(Linear synchronous transit,线性同步转变)，这个方法假设反应过程中，反应物结构的每个坐标都是同步、线性地变化到产物结构。如果反应物、产物的坐标分别以向量A、B表示，则反应过程中的结构坐标可表示为(1-x)*A+x*B，x由0逐渐变到1代表反应进度。注意LST并不是指反应中原子在真实空间上以直线运动，只有笛卡尔坐标下的LST才是如此，在内坐标下的LST，原子在真实空间中一般以弧线运动。以LST的假设，反应路径在其所用坐标下的势能面图上可描述为一条直线，LST给出的过渡态就是这条直线上能量最高点（图3的点1）。LST的问题也很显著，其假设的坐标线性变化多数是错误的，绘制在势能面图上也多数不会是直线，故给出的过渡态也有较大偏差，容易带两个或多个虚频。

比LST更合理的是QST(quadratic synchronous transit,二次同步转变)，它假设反应路径在势能面上是一条二次曲线。QST在LST得到的过渡态位置上，对LST直线路径的垂直方向进行线搜索找到能量极小点A（图3的点2）。QST给出的反应路径可以用经过反应物、A、产物的二次曲线来表示，如果这条路径上能量最大点的位置恰为A，则A就是QST方法给出的过渡态；如果不是，则以最大点作为过渡态。若想结果更精确，可以再对这个最大点向垂直于路径的方向优化，再次得到A并检验，反复重复这个步骤，逐步找到能量更低、更准确的过渡态。

QST方法在计算能力较低的年代曾是简单快速的获得过渡态和反应路径的方法，然而如今看来其结果是相当粗糙的，已极少单独使用，可以将其得到的过渡态作为AH法的初猜。

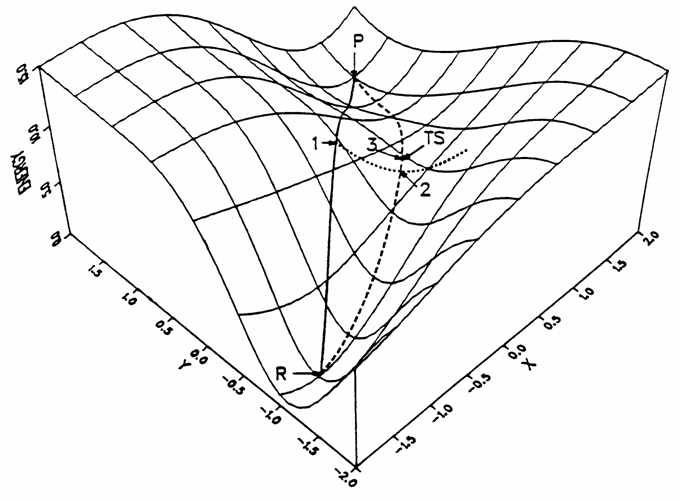
[图3]LST与QST方法示意图

2.2.2 STQN方法(Combined Synchronous Transit and Quasi-Newton Methods)

STQN是ST与QN方法的结合（更准确地说是与EF法的结合）。但不要简单认为是按顺序独立执行这两步，即认为“先利用反应物和产物结构以ST方法得到粗糙过渡态，再以之作为初猜用QN法精确寻找过渡态”是错误的。STQN方法大意是：使结构从低能量的反应物出发，以ST路径在当前位置切线为引导，沿着LST或QST假设的反应路径行进（爬坡步），目的是使结构到达假设路径的能量最高处附近（真实过渡态二次区域附近）。当符合一定判据时就转换为QN法寻找精确过渡态位置（EF步）。下面介绍具体步骤。

先说明后面用到的切线的定义：STQN当中的LST路径与前面ST部分介绍的LST路径无异，都是直线，切线T在优化中是不变的，就是反应物R指向产物P的单位向量。STQN方法中的QST路径定义与ST方法介绍的不同，走的不是二次曲线而是圆形的一段弧，如图4所示。这个圆弧经过R、P以及优化中的当前步位置X，切线就是圆在X处的单位切线向量，圆弧和切线在每一步都是变化的。虽然QST路径比LST更为合理，但对于QSTN方法，QST路径在收敛速度和成功机率上的优势并不显著。

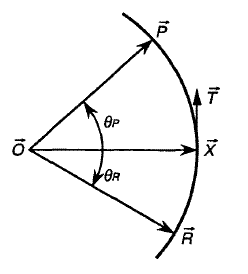
[图4]STQN对QST路径的定义

STQN每一步执行内容如下：(1)首先重新计算或用QN法更新Hessian。(2)按上述方法计算当前位置处的切线。(3)决定这一步是爬坡步还是EF步。如果是优化的第前两步，则一定认为是爬坡步，因为此时离过渡态区域还较远，应当先爬坡。如果是第3、4步，则估算出在切线方向的位移，超过一定标准就是爬坡步，否则说明爬得差不多了就进入EF步找过渡态。如果是第5步之后，一般已离过渡态区域较近，故一定认为是EF步。(4)如果是爬坡步，则在切线方向上移动（将切线方向作为EF方法所跟踪的振动方向来计算位移大小）。如果是EF步，首先计算Hessian各个本征向量的与切线重叠情况，如果有重叠大于0.8的本征向量，则以EF法跟踪本征值最大的本征向量来移动，相当于继续向上爬。如果没有大于0.8的，就跟踪最小本征值的本征向量移动来寻找过渡态。(5)步长长度若大于标准则调小，默认0.3 bohr。(6)根据预置受力、位移标准判断是否已收敛，收敛则结束循环。

注意，ST方法中具体包含LST和QST两种方法，STQN也用到了LST和QST两种反应路径的假设。高斯中的LST方法指的是ST中的LST方法，而QST2/3指的是利用QST路径假设的STQN方法，它们原理上截然不同，不要混淆。高斯中的QST2只需输入反应物和产物结构，通过在冗余内坐标下反应物与产物结构间插值得到STQN的初始步结构X。QST3需额外输入猜测的过渡态，它直接作为X，一般比QST2效果更好。对于经验不足的用户，用STQN方法往往比只提供过渡态初猜的方法更为适合。注意产物和反应物应当使用同样方法同样基组进行优化，如果是多分子比如A+B=C+D这样的反应，应当优化A和B/C和D的复合物作为输入的产物/产物，而不是单独优化A、B然后拼到一起，因为形成范德华复合物后孤立的分子会有一定构象改变，能量也低于它们孤立状态的加和。

2.2.3 赝坐标法(pseudo reaction coordinate)

也称为坐标驱动法(Coordinate Driving)。这个方法在高斯中就是柔性扫描(Relaxed Scan)，即扫描一个变量，但每一步对其它变量自动进行优化，每一步得到的结构就是在这个变量为一定值情况下的最优结构。赝坐标法扫描的是反应物转变到产物过程中的关键坐标，比如扫描化学键断裂/生成反应中的键长。扫描的结果就是近似的IRC，可以再将能量最高点作为初猜找过渡态，或者用更小的步长再次扫描能量最高点附近找更精确的过渡态结构。这个找过渡态方法实际上用的是能量极小化优化过程，由于这样的算法比寻找过渡态的算法更为稳健，所以赝坐标法是颇可靠的，其它方法失败时可考虑这种方法。

这个方法缺点是费时间，而且不适合通向过渡态路径中反应区域涉及多个坐标变化的反应过程，因为自定义扫描的内容很难全面、准确考虑到这些坐标变量的变化，结果难以说明问题，没有考虑进去的关键变量容易产生滞后效应(hysteresis effect)。比如乙烷由交叉构象变化到另一个交叉构象，需要经历重叠构象的过渡态，会涉及到三个HCCH二面角同时由60度变化到0度，如果用赝坐标法只扫描其中一个HCCH由60度变到0度，则每一步其它两个HCCH角一定会大于这个扫描的二面角，与实际不符。这是因为这两个角越小，分子的能量越高，每一步自动优化的时候它们更倾向于保持在大角度。最终到达过渡态时，所扫描的二面角到达了0度，另外两个二面角却大于0度，说明它们的运动比实际的过程滞后了。由于滞后效应，从反应物和产物两个方向扫描同相同的坐标，得到的路径也不同。上述简单的反应此方法滞后效应尚且严重，对于复杂变化，这种效应导致的问题更难以预测。故此方法确定的IRC、过渡态不可靠，只建议对简单的反应使用这种方法，扫描变量的选择注意避免滞后效应。

在高斯中此方法可以使用opt=modredundant或Opt=Z-matrix结合分子结构部分标记的扫描变量来实现。例如使用opt=modredundant并在分子结构末尾写上A 3 2 1 S 10 1.000000来指定3 2 1原子组成的角度进行柔性扫描，共10步，每步1.0度。如果不熟悉，也可以很方便地在GaussView里的冗余坐标编辑器里面添加要柔性扫描的变量。

如果只执行常规的某个变量的扫描，比如高斯中的scan来找能量最高点作为初猜结构，对于简单体系可行，但对于复杂体系，这样忽略了此变量的变化导致分子其它部分结构的驰豫，如此得到的能量最高点作为过渡态初猜很不可靠，因为势能中掺入了不合理的结构造成的能量升高，使势能曲线形状改变。

2.2.4 DHS方法(Dewar-Healy-Stewart，亦称Saddle方法)与LTP方法(Line-Then-Plane)

DHS方法中第一步将反应和产物分别作为A点和B点，确定哪个点能量低，比如A比B低，就把A点的结构向B点稍微做调整(~5%)得到A'，然后限制变量空间中A'与B的距离不变（即在超球面上）对A'进行优化得到A''。将A''与B当作下一步的起始点A与B，重复上述方法。这样反复进行迭代，若以序号n代表第n次得到的A''或B''，会依次得到例如A''(1)、A''(2)、B''(1)、A''(3)......直到A与B十分接近时才停止迭代，此位置就是过渡态。将得到的全部A''(n)按序号n依次连接，B''(n)也按序号依次连接，再将序号最大的A''(n)与B''(n)连接，得到的就是近似的IRC。LTP与DHS方法基本一致，不同的是每步是在垂直于A'与B连线的超平面上优化。DHS方法虽然可以很快地走到过渡态附近的位置，但是越往后每步的AB距离缩近也越少，故并不能有效率地贴近过渡态。然而每步的在连线上调整的距离不可过大，否则可能造成一侧的点跨过过渡态势垒跑到另一侧得到错误结果。

[图5]DHS方法示意图

2.2.5 Ridge方法

第一步时将反应物、产物作为A点和B点，在其LST的路径上找到能量最大点C，然后在AC与BC直线上相距C为s的位置上分别设一点A'和B'，将A'与B'分别沿着此处势能面负梯度优化p距离，将得到的A''与B''作为下一步的A和B。反复进行这个步骤，收敛后C的位置就是过渡态位置。s和p是计算过程中动态调节的参数，对结果影响较大，它们应当随C逐渐接近过渡态而减小，可设若当前步的C能量高于上一步的C，则减小p至原先一半；若s与p的比值大于某个数值，s也减半。Ridge方法的缺点是接近过渡态时效率较低，可以当C进入过渡态二次区域后改用QN法来加快收敛。也可以结合DIIS法，速度比原先有一半以上的提升，效率有时还高于基于二阶导数的方法，而且在某些势能面非常平坦的体系比二阶导数方法更可靠。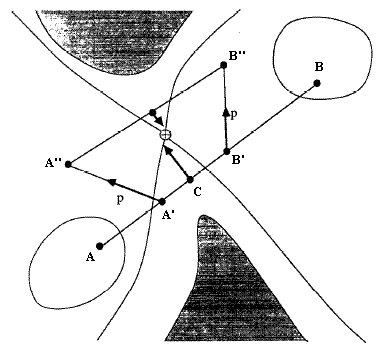

[图6]Ridge方法示意图

2.2.6 Step-and-Slide方法

使产物和反应物的结构同时顺着LST描述的路径相对移动(step步)，直到它们的能量都等于某个预先设定的能量，然后让这两个结构在它们当前所在的势能等值面上滑动(slide步)，使二者结构在坐标空间中的距离最小。重复上述step和slide步骤，最终当两个结构碰上，这个位置就是过渡态。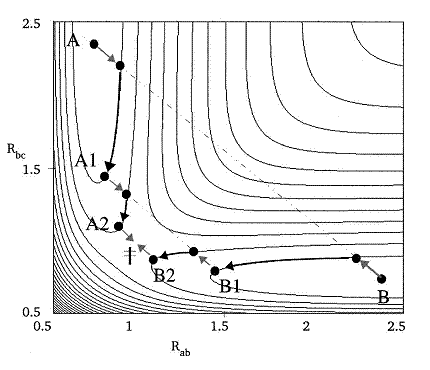

[图7]Step and Slide方法示意图

2.2.7 Müller-Brown方法

见下文IRC算法相应部分

2.2.8 CI-NEB、ANEBA方法

见下文“寻找过渡态的chain-of-state方法”相应部分

2.3 基于反应物结构的算法

2.3.1 最缓上升法(least steep ascent,shallowest ascent)

由反应物结构到达过渡态结构的过程是沿着势能面最容易行进的路径进行的（不考虑动力学问题），这个途径一般比其它方向要缓和，所以由反应物结构开始，沿着势能面最缓的方向逐渐往上爬，往往可以沿着MEP到达过渡态。但要注意这条路径时常与从过渡态沿最陡下降路径所走出的MEP并不一致，因此原理上此法不能保证一定能到达过渡态。图8描述的是LEPS势结合谐振势的势能面，最缓上升法所走的黑色粗曲线严重不符合实际MEP（黑点所示路径），而且曲线是中断的。此法也可能走到与此平衡结构相连的其它过渡态，而非预期的过渡态。还容易因为步长问题导致走到中途时跑到另外一条错误路径上，虽然设小步长能得到解决，但是需要花费更长时间。因为种种问题，这个方法使用较少。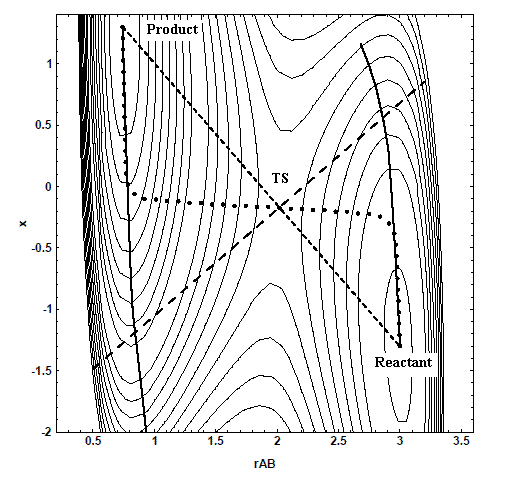

[图8]势能面上最缓上升法所走的路径（黑色粗曲线）

2.3.2 本征向量/本征值跟踪法(eigenvector/eigenvalue following,EF。也称mode walking/mode following/Walking up valleys)

名字中的本征向量、本征值是指Hessian矩阵的本征向量和本征值，经过质量加权后就对应于简正振动模式和相应的力常数，所以也叫模式跟踪。由于平衡结构越过势垒发生反应的能量主要来自分子某振动模式提供的动能，由此可以想象，由稳定结构沿着此振动矢量方向步进，就能够找到过渡态，经历的路径就是反应路径。这种方法需要首先对平衡结构进行振动分析，由用户最初指定一个可能指向过渡态的振动模式。由于由平衡态出发，通向过渡态路径势能面平缓，此方向曲率一般小于其它方向，故一般跟踪力常数最小的振动模式（高斯中默认），这也叫最低模式(Low-Mode)，这个模式的力常数一开始是正值（频率为实数），经过势能面拐点后变为负数（频率为虚数），直至到达过渡态。每走一步后重新计算Hessian矩阵获得新的振动模式和对应力常数，如果跟踪的是最低的模式，仍取力常数最小的模式继续跟踪；如果跟踪的是其它振动模式，就取与上一步所跟踪的振动模式重叠最大的模式继续跟踪。重复执行，直到符合收敛标准为止。

如果一个结构涉及到多个过渡态，则跟踪不同的本征向量有可能得到不同的过渡态，即便所跟踪的不是最低模式，当接近过渡态后也会成为最低的模式。此方法也可以直接由过渡态初猜结构开始跟踪，或者说EF方法是一种不需要初猜在过渡态二次区域内的寻找过渡态的方法。由稳定结构通过EF方法跟踪至过渡态相对与直接给出初猜显然更为费时，但对于不能预测过渡态结构的情况下往往是有用的。LMOD法搜索构象也是基于这一原理，不断地根据低频振动方向越过构象转变的过渡态到达新的构象。

最初的EF方法只是简单地沿所跟踪的振动模式移动来升高能量。高斯中opt=(EF,TS)方法还使结构同时在其余方向上沿能量更低的方向移动，其实它用的就是已介绍的P-RFO法，所跟踪的模式用独立计算的λ的最大解，其它的模式使用相同的另外计算的λ的最小解。由于Berny方法寻找过渡态已经包含了P-RFO步，所以EF方法实际上也已经包含在内了，除非要用到跟踪特定模式等功能时才有使用的必要。

2.3.3 ARTn(activation-relaxation technique nouveau)

此方法主要用于研究无序材料的在能量面上由极小点穿过过渡态到达其它极小点的过程，解决由于势垒高而难以用MD和MC方法研究的问题。方法分两步，(1)将初始结构由极小点位置激活并收敛到过渡态(activation步)，(2)由过渡态通过常规的能量极小化算法寻找极小点(relaxation步)。(1)中的每一步中在任意方向上移动结构，然后在垂直于走过的路径方向的超平面上做能量极小化，反复执行，直到Hessian矩阵出现一个负本征值为止。之后进入收敛至鞍点的步骤，在最小本征值的方向上沿受力反方向移动，其余方向根据受力移动，最终将找到一阶鞍点。由于大体系Hessian矩阵本征值求解困难，此方法中使用Lanczos算法快速求解最低本征值和本征向量。ART法可以获得与初始极小点相连的许多过渡态。

2.3.4 梯度极值法(Gradient extremal,GE)

梯度极值路径连接的是每一个能量等值线（高维情况为超曲面）上的梯度的模|g|为极大或极小值的点（相对于同一等值线上的其它点的梯度模来说）。因为势能面的每一点的梯度垂直于此点等值线的切线，故梯度模极值点的位置相当于垂直于等值线方向上等值线间隔比处在相同等值线上相邻的点更远或更近。|g|的极值与g^2一致，设势能函数为f，限制所在等值线能量为一常数k，通过拉格朗日乘子法求g^2的极值▽[g^2-2λ(f-k)]=0，执行微分后写成Hg=λg，可知梯度极值点的梯度方向等于此点Hessian矩阵某一本征向量。由于势能面上每个驻点必有一条或多条梯度极值路径通过而互相构成网络（但任意驻点间不一定有梯度极值路径直接相连），所以系统地跟踪梯度极值路径是一种获得势能面上全部驻点的方法，目前已有几种跟踪算法，然而即便对于简单体系，梯度极值路径数目也极多，尤其是包含对称性情况下。由极小点跟踪梯度极值路径也能够用于寻找过渡态，但极小点未必与过渡态通过梯度极值路径直连，且此方法并不能控制要寻找哪类驻点，故为了寻找过渡态可能需要从多个其它驻点跟踪多个梯度极值路径，计算量很大，所以单纯为了寻找过渡态而使用这种方法不切实际。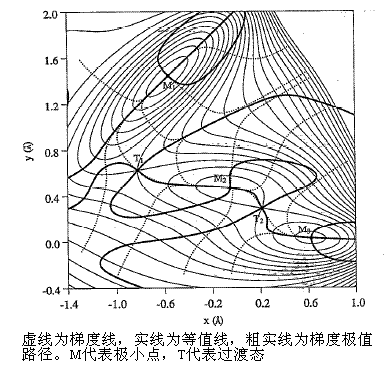

[图9]梯度极值路径示意图

2.3.5 约化梯度跟踪(reduced gradient following,RGF)

这个方法同梯度极值法一样可以得到包括过渡态、极小点在内的各种驻点。设势能面为N维，此方法将跟踪N条路径，其中第i条(i=1,2,3...N)路径只有在第i维上梯度不为0，而其它N-1个维度上皆为0，故称为约化梯度。这样的路径交汇的位置，就是所有维度上梯度皆为0的位置，即驻点。例如简单的二维情况E(x,y)=x^3+y^3-6xy，跟踪的RGF方程就是Ex(x,y)=3x^2-6y=0和Ey(x,y)=3y^2-6x=0，前者仅y方向梯度不为0，后者仅x方向梯度不为0，相交得到的驻点为一个一阶鞍点和一个极小点。也可以使用原始坐标组合的正交坐标系，例如跟踪仅x+y和仅x-y方向上梯度不为0的两条路径。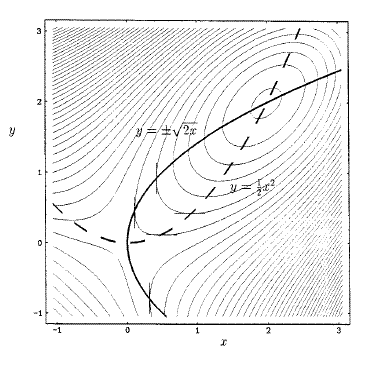

[图10]x^3+y^3-6xy面上约化梯度路径示意图

跟踪约化梯度的步进算法是第m点的坐标x(m+1)=x(m)+StL*x'(m)/|x'(m)|。StL是步长，x'(m)/|x'(m)|代表路径切线方向单位向量。x'可以通过H'x'=0方程以QR分解法获得，其中H'与Hessian矩阵唯一不同的是，若当前跟踪的是仅第k维梯度不为0的约化梯度路径，则H'没有Hessian矩阵的第k行。一般起始步由某驻点开始，此步准确计算Hessian，步进过程中Hessian可用前述的DFP方法修正。每步检验所跟踪方向上的朝向下一个驻点的牛顿步步长，若小于标准则停止，并且再精确计算一次Hessian以确认此驻点是什么类型。每次走步的结果如果在数值上与“仅某维度上梯度为0”条件符合较好，可以动态增加步长，类似AH法的置信半径概念，如果相差较大，则调用校正步（后期方法将校正步合并入步进步，改善了效率和稳定性）。

这个方法计算量也很大，而且也无法指定要搜索的驻点的类型，所以不适合独立用作寻找过渡态。

2.3.6 等势面搜索法(Isopotenial Searching)

如果将反应物位置附近的势能面比做一个湖，这个方法可以看作逐渐往湖里面灌水，由于过渡态能量比周围地方更低，所以随着水位（势能）逐渐升高，水最先流出来的地方就是过渡态。继续灌水，随着水位继续升高，还可以找到其它能量更高的过渡态。

具体实现的方法是：首先最小化反应物的能量E0，在反应物位置附近设置一些测试点，可以随机也可以根据经验设定，作为“水位”来检测是否已到达过渡态能量。然后设定目标能量E(target)，一般高于E0几百KJ/mol。计算那些测试点的能量和势能梯度，检查其能量与E(target)的差的绝对值，若大于10KJ/mol，即没达到目标水位，就让它们沿着梯度方向行进以提升能量，之后再次检查是否符合条件，直到小于10KJ/mol，即已到达目标水位，就对这些点进行人工的检查，包括结构、成键分析等，考察在E(target)时是否已经达到或超过了过渡态的能量。如果找到了过渡态，就调整这些点的位置继续找别的过渡态；如果未找到，就提高E(target)并且调测试点整位置以增大找到过渡态的概率，然后再沿着梯度方向提升测试点的能量并进行接下来的检测，反复如此。

上述提到的“调整点的位置”有很多算法，但主要都是使那些测试点在垂直于梯度，即在等值面上移动。因为测试点无法密集覆盖整个等势面，受计算能力制约其数目有限的，很难有哪个点随着E(target)的提升而移动后恰好落在过渡态的位置。直到E(target)提升到有测试点可判断为过渡态时，其能量一般已高出实际过渡态很多。所以使用此方法得到的过渡态能量与初始点位置和调整点位置的算法都有很大关系，一般都显著偏高，甚至不能找到过渡态，可尝试以不同初始位置和调整算法重新执行以改善结果。等势面搜索法适合在只有反应物结构而难以预测过渡态和产物结构的情况下寻找过渡态，例如预测质谱中分子的可能裂解的方式，有时还可能找到全新未曾考虑到的反应机理。但是此方法的结果很粗糙，而且计算量极大，尤其是大分子的高维势能面，有限的测试点很容易漏掉许多重要过渡态。

2.3.7 球形优化(Sphere optimization)

在几何参数的变量空间上，以反应物或产物为中心，在不断增加半径的超球面上做能量最小化。将相邻球面上得到的能量极小点相连接，就得到一条由反应物或产物为起点的低能量的路径，可做为IRC（未必正确，考虑图8的势能面），并由此找到过渡态。如果每个球面上可以找到多个极小点，则连接后有可能得到多条反应路径。此法若以坐标驱动法为类比，此方法就是对几何参数空间中反应物或产物结构代表的点的距离进行柔性扫描。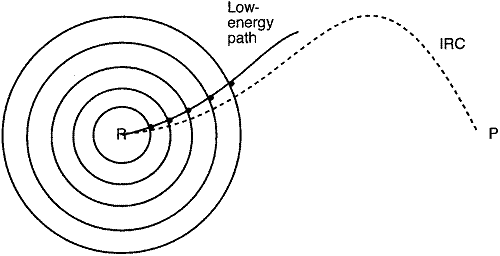

[图11]球形优化示意图

2.4 全势能面扫描

当一切方法都不能找到过渡态，全势能面扫描是最终途径。由于扫描得到的势能面格点是离散的，可通过插值提高格点密度以增加精度。得到势能面后，就可以通过一些算法找到过渡态，例如用这些点拟合出解析表达式，然后用标准微分方法找过渡态。但全势能面扫描极为昂贵，内坐标下需要计算X^(3N-6)次（X代表每个变量扫描步数），只限于反应中仅涉及几个自由度的势能面扫描，往往不得不考虑更低级的方法如半经验或者分子力学，变量稍多的体系则完全不能实现。全势能面扫描的结果还提供了过渡态位置以外结构的信息，例如可以用于研究反应路径、用于构象搜索等。

3.过渡态相关问题

3.1 无过渡态的反应途径(barrierless reaction pathways)

并非所有反应途径都需要越过势垒，这类反应在很低的温度下就能发生，盲目找它们的过渡态是徒劳的。常见的包括自由基结合，比如甲基自由基结合为乙烷；自由基向烯烃加成，比如甲基自由基向乙烯加成成为丙基自由基；气相离子向中性分子加成，比如叔碳阳离子向丙烯加成。等等。

3.2 Hammond-Leffler假设

过渡态在结构上一般会偏向反应物或者产物结构一边。Hammond-Leffler假设对预测过渡态结构往哪个方向偏是很有用的，意思是反应过程中，如果两个结构的能量差异不大，则它们的构型差异也不大。由此可知对于放热反应，因为过渡态能量与反应物差异小，与产物差异大，故过渡态结构更偏向反应物，相反，吸热反应的过渡态结构更偏向产物。所以初猜过渡态结构应考虑这一问题。

3.2 对称性问题

如果已经明确地知道过渡态是什么对称性，而且对称性高于平衡态对称性，且可以确信在这个高对称性下过渡态是能量最低点，则可以强行限制到这个对称性之后进行几何优化，几何优化算法比寻找过渡态算法方法更可靠。比如F+CH₃F-->FCH₃+F这个SN2反应，过渡态就是伞形翻转的一刻，恰为高对称性的D3h点群，而反应路径上的其它结构对称性都比它低，所以在D3h点群条件下优化，得到的能量最低点就是过渡态。

如果过渡态对称性不确定，则找过渡态计算的时候不宜设任何对称性，否则若默认保持了平衡态下的对称性，得到的此对称下的过渡态并不是真正的过渡态，容易得到二阶或高阶鞍点。

3.3 溶剂效应

计算凝聚态条件下过渡态的性质，必须考虑溶剂效应，它明显改变了势能面。一般对过渡态的结构影响较小，但对能量影响很大。有时溶剂效应也会改变反应途径，或产生气相条件下没有的势垒。溶剂条件下，上述寻找过渡态的方法依然适用。应注意涉及到与溶剂产生氢键等强相互作用的情况，隐式溶剂模型是不适合的，需要用显式溶剂考察它对过渡态的影响，即在输入文件中明确表达出溶剂分子。

3.4 计算过渡态的建议流程

一般建议的流程是：
1 用中等计算级别找过渡态，如B3LYP/6-31G*。
2 用相同水平对上一步找到的过渡态做振动分析，检验是否仅有一个虚频，以及观看其振动模式的动画来考察振动方向是否连接反应物与产物结构。有必要时可以做IRC进一步检验。
3 用高级别方法（如双杂化泛函或CCSD(T)结合def2-TZVP等中/高质量基组）对第1步得到的过渡态结构计算能量。
另外，如果对B3LYP/6-31G*这样级别的过渡态的精度还不够满意（虽然通常已经够了），可以以这个级别的过渡态为初猜结构，改用更好的方法和基组去进一步优化过渡态结构。

4.内禀反应坐标(intrinsic reaction coordinate,IRC)

MEP指的是势能面上，由一个点到达另一个点的能量最低的路径，满足最小作用原理。若质量权重坐标下的MEP连接的是反应物、过渡结构和产物，则称为IRC。所谓质权坐标在笛卡儿坐标下即r(i,x)=sqrt(m(i))*R(i,x)，m(i)为i原子质量，R(i,x)为i原子原始x方向坐标，同样有r(i,y)、r(i,z)。IRC描述了原子核运动速度为无限小时，质权坐标下由过渡态沿着势能负梯度方向行进的路径（最陡下降路径），其中每一点的负梯度方向就是此处核的运动方向，在垂直于路径方向上是能量极小点。注意质量权重和非权重坐标下的路径是不一样的。

IRC基本上可看作0K时的实际在化学反应中原子核所走的路径（但这并不严格，因为由于振动零点能的关系，即便0K下也有核运动故会略微偏离IRC），温度较低时IRC也是一个很好的近似。但是当温度较高，即核动能较大时，实际反应路径将明显偏离IRC，而趋于沿最短路径变化，即便经历的是势能面上能量较高的的路径，这时就需要以动力学计算的平均轨迹来表征反应路径。

5.IRC算法

5.1 最陡下降法(Steepest descent)

最简单的获得IRC的方法就是固定步长的最陡下降法，由过渡态位置开始，每步沿着当前梯度方向行进一定距离直到反应物/产物位置，也称Euler法。由于最陡下降法及下文的IMK、GS等方法第一步需要梯度，而过渡态位置梯度为0，所以第一步移动的方向沿着虚频方向。最陡下降方法与IRC的本质相符，但是此法实际得到的路径是一条在真实IRC附近反复震荡的曲折路径，而非应有的平滑路径，对IRC描述不够精确。虽然可以通过更小的步长得以一定程度的解决，但是太花时间，对于复杂的反应机理，需要更多的点。也可以通过RK4(四阶Runga-Kutta)来走步，比上面的方法更稳定、准确，但每步要需要算四个梯度，比较费时。

5.2 IMK方法(Ishida-Morokuma-Komornicki)

它是最陡下降法的改进，解决其震荡问题。首先计算起始点X(k)的梯度g(k)，获得辅助点X'(k+1)=X(k)-g(k)*s，其中s为可调参数。然后计算此点梯度g'(k+1)，在g(k)与-g'(k+1)方向的平分线上（红线所示）进行线搜索，所得能量最小点即为X(k+1)，之后再将X(k+1)作为上述步骤的X(k)重复进行。整个过程类似先做最陡下降法，然后做校正。此方法仍然需要相对较小的步长，获得较精确IRC所需计算的点数较多。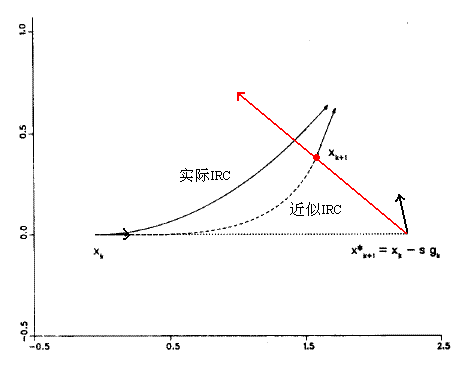

[图12]IMK方法示意图

Schmidt，Gordon，Dupuis改进了IMK的三个细节，使之更有效率、更稳定。(1)将X'(k+1)的确定方式改为了X(k)-g(k)/|g(k)|*s，即每一步在负梯度方向上行进固定的s距离，与梯度大小不再有关。(2)线搜索步只需在平分线上额外计算一个点的能量即可，这个点和X'(k+1)点的能量以及g'(k+1)在此平分线上的投影三个条件作联立方程即可解出曲线方程，减少了计算量。IMK原始方法则需要在平分线上额外计算两个点的能量与X'(k+1)的能量一起拟和曲线方程。(3)第一步在过渡态位置的移动距离Δq如此确定：ΔE=k*(Δq^2)/2，k为虚频对应的力常数，ΔE为降低能量的期望值（一般为0.0005 hartree），这样可避免在虚频很大的鞍点处第一步位移使能量降低过多。

5.3 Müller-Brown方法

这是通过球形限制性优化找IRC的方法。首先将过渡态和能量极小点位置定义为P1和P2，由P1开始步进，当前步结构以Q(n)表示。每一步，在相距Q(n)为r距离的超球面上用simplex法优化获得能量极小点Q'（图中绿点），优化的起始点是Q(n-1)Q(n)与Q(n)P2方向的平分线b上距Q(n)为r距离的位置S（红点）。若Q(n)Q'与Q(n)P2的夹角较小，则Q'可当作是下一步位置Q(n+1)。如此反复，直到符合停止标准，比如下一步能量比当前更高（已走过头了）、与P2距离已很近（如小于1.2r）、或者与P2方向偏离太大（P1与P2点通过此法无法找到IRC）。最终所得到全部结构点依次相连即为近似的IRC，减小步长r值可使结果更贴近实际IRC。基于此方法也可以用于寻找过渡态，先将反应物和产物作为P1和P2，将二者距离的约2/3作为r，由其中一点在P1-P2连线上相距其r位置为初始位置进行球形优化得到O点，在O与P1、O与P2上也如此获得P1'与P2'，根据P1、P1'、O、P2'、P2的能量及之间距离信息以一定规则确定其中哪两个点作为下一步的P1和P2，确定新的P1和P2后重复上述步骤，直至P1与P2十分接近，即是过渡态。此方法计算IRC可以步长可设得稍大，第一步不需要费时的Hessian矩阵确定移动方向，缺点是获得的路径曲率容易有问题，对于曲率较大的反应路径需要减小步长。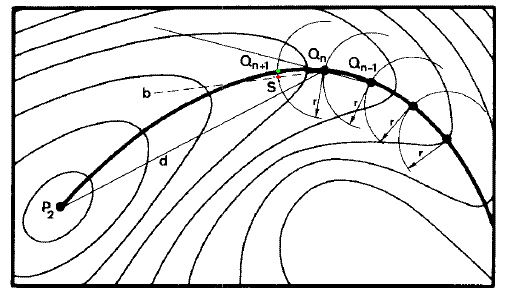

[图13]Müller-Brown方法示意图

5.4 GS(Gonzalez-Schlegel)方法

这是目前很常用，也是Gaussian使用的方法，见图14。首先计算起始点X(k)的梯度，沿其负方向行进s/2距离得到X'(k+1)点作为辅助点。在距X'(k+1)点距离为s/2的超球面上做限制性能量最小化，找到下一个点X(k+1)。因为这个点的负梯度（黑色箭头）在弧方向上分量为0，故垂直于弧，即其梯度方向在X'(k+1)到X(k+1)的直线上。这必然可以得到一段用于描述IRC的圆弧（虚线），它通过X(k)与X(K+1)点，且在此二点处圆弧的切线等于它们的梯度方向，这与IRC的特点一致，这段圆弧可以较好地（实线）。之后再将X(k+1)作为上述步骤的X(k)重复进行。

GS方法对IRC描述得比较精确，在研究反应过程等问题中，由于对中间体结构精度有要求，GS是很好的选择，而且用大步长可以得到与小步长相近的结果，优于IMK、Müller-Brown等方法。若只想得到与过渡态相连的反应物和产物结构，或者粗略验证预期的反应路径，对IRC精度要求不高，使用最陡下降法往往效率更高，尽管GS可以用更大步长，但每步更花时间。

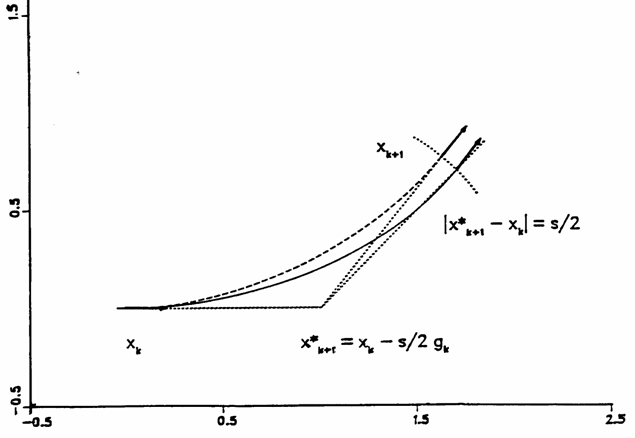
[图14]GS方法示意图

除上述外，IRC也可以通过已提及的EF、最缓上升法、球形优化等方法得到，它们的好处是不需要事先知道过渡态的结构。赝坐标法除了简单的反应以外，只能得到近似的IRC，由于结构的较小偏差会带来能量的较大变化，容易引入滞后效应，所以这样得到的势能曲线难以说明问题。

6. chain-of-states方法

这类方法主要好处是只需要提供反应物和产物结构就能得到准确的反应路径和过渡态。首先在二者结构之间以类似LST的方式线性、均匀地插入一批新的结构（使用内坐标更为适宜），一般为5~40个，每个结构就是势能面上的一个点(称为image)，并将相邻的点以某种势函数相连，这样它们在势能面上就如同组成了一条链子。对这些点在某些限制条件下优化后，在势能面上的分布描述的就是MEP，能量最高的结构就是近似的过渡态位置。

6.1 Drag method方法

这个方法最简单，并不是严格的chain-of-states方法，因为每个结构点是独立的。插入的结构所代表的点均匀分布在图8所示的短虚线上，也可以在过渡态附近位置增加点的密度。每个点都在垂直于短虚线的超平面上优化，在图中就是指平行于长虚线方向优化。这种方法一般是奏效的，但也很容易失效，图8就是一例，优化后点的分布近似于从产物和反应物用最缓上升法得到的路径（黑色粗曲线），不仅反应路径错误，而且两段不连接，与黑色小点所示的真实MEP相距甚远（黑色点是用下文的NEB方法得到的）。目前基本不使用此方法。

6.2 PEB方法(plain elastic band)

这是下述Chain-of-state方法的基本形式。也是在反应物到产物之间插入一系列结构，共插入P-1个，反应物编号为0，产编号物为P。不同的是优化不是对每个点孤立地优化，而是优化一个函数，每一步所有点一起运动。下文用∑[i=1,P]X(i)符号代表由X(1)开始加和直到X(P)。PEB函数是这样的：S(R(1),R(2)...R(P-1))=∑[i=1,P-1]V(R(i)) + ∑[i=1,P]( k/2*(R(i)-R(i-1))^2 )。其中R(i)代表第i个点的势能面上的坐标，V(R(i))是R(i)点的能量，k代表力常数。优化过程中反应物R(0)和产物R(P)结构保持不变，优化此函数相当于对一个N*(P-2)个原子的整体进行优化，N为体系原子数。

优化过程中，式中的第一项目的是让每个点尽量向着能量极小的位置移动。第二项相当于将相邻点之间用自然长度为0、力常数为k的弹簧势连了起来，目的是保持优化中相邻点之间距离均衡，避免过大。当只有第一项的时候，函数优化后结构点都会跑到作为能量极小点的反应物和产物位置上去而无法描述MEP，这时必然会有一对儿相邻结构点距离很大。当第二项出现后，由于此种情况下弹簧势能很高，在优化中不可能出现，从而避免了这个问题。drag method法在图8中失败的例子中，也有一对儿相邻结构点距离太远，所以也不会在PEB方法中出现。简单来说，PEB方法就是保持相邻结构点的间距尽量小的情况下，优化每个结构点位置。可以近似比喻成在势能面的模型上，将一串以弹簧相连的珠子，一边挂在反应物位置，另一边挂在产物位置，拉直之后松手，这串珠子受重力作用在模型上滚动，停下来后其形状可当作MEP，最高的位置近似为过渡态。

但是PEB方法的结果并不能很好描述MEP。图15描述的是常见的A、B、C三原子反应的LEPS势能面，B可与A或C成键，黑色弧线为NEB方法得到的较真实的MEP。左图中，在过渡态附近PEB的结构点没有贴近MEP，得到的过渡态能量过高，称为corner-cutting问题。这是因为每点间的弹簧势使这串珠子僵硬、不易弯曲，由图15右图可见，R(i)朝R(i-1)与R(i+1)方向都会受到弹簧拉力，其合力牵引R(i)，使R(i-1)、R(i)、R(i+1)的弧度有减小趋势。如果将弹簧力常数减小以减弱其效果，就会出现图15中间的情况，虽然结构点贴近了MEP，但相邻点间距没有得到保持，过渡态附近解析度很低，错过了真实过渡态，若以能量最高点作为过渡态则能量偏低，这称为sliding-down问题。可见弹簧力常数k的设定对PEB结果有很大影响，为权衡这两个问题只能取折中的k，但结果仍不准确。

[图15]LEPS势能面上不同k值的PEB结果

6.3 Elber-Karplus方法

与PEB函数定义相似。第一项定义为1/L*∑[i=1,P-1]( V(R(i))*d(i,i-1) )，其中L为链子由0点到P-1点的总长，d(i,i+1)为R(i)与R(i+1)的距离，此项可视为所有插入点总能量除以点数，即插入点的平均能量。第二项为γ*∑[i=1,P](d(i,i-1)-<d>)^2，其中<d>代表相邻点的平均距离，是所有d(i,j)的RMS。此项相当于将弹簧自然长度设为了当前各个弹簧长度的平均值，由γ参数控制d(i,j)在平均值上下允许的波动的范围。此方法最初被用于研究蛋白质体系的构象变化。

6.4 SPW方法(Self-Penalty Walk)

在Elber-Karplus方法的基础上增加了第三项互斥项，∑[i=0,P-1]∑[i=j+1,P-1]U(ij)，其中U(ij)=ρ*exp(-d(i,j)/(λ*<d>))，<d>定义同上。此项相当于全部点之间的“非键作用能U(ij)”之和，不再仅仅是相邻点之间才有限制势。任何点之间靠近都会造成能量升高，可以避免Elber-Karplus方法中出现的在能量极小点处结构点聚集、路径自身交错的问题，能够使路径充分地展开，确保过渡态区域有充足的采样点。式中ρ和λ都是可调参数来设定权重。此外相对与Elber-Karplus方法还考虑了笛卡儿坐标下投影掉整体运动的问题。

6.5 LUP方法(Locally Updated planes)

特点是优化过程中，只允许每个结构点R(i)在垂直于R(i-1)R(i+1)向量的超平面上运动。由于每步优化后R(i-1)与R(i+1)连线方向也会变化，故每隔一定步数重新计算这些向量，重新确定每个点允许移动的超平面。但是LUP缺点是结构点之间没有以上述弹簧势函数相连来保持间隔，容易造成结构点在路径上分布不均匀，甚至不连续，还可能逐渐收敛至两端的极小点。

6.6 NEB方法(Nudged Elastic Band)

NEB方法集合了LUP与PEB方法的优点，其函数形式基于PEB。从PEB方法的讨论可以看出，弹簧势是必须的，它平行于路径切线（R(i)-R(i-1)与R(i+1)-R(i)矢量和的方向）的分量保证结构点均匀分布在MEP上来描述它；但其垂直于路径的分量造成的弊端也很明显，它改变了这个方向的实际的势能面，优化后得到的MEP'就与真实的MEP发生了偏差，造成corner-cutting问题。解决这个问题很简单，在NEB中称为nudge过程，即每个点在平行于路径切线上的受力只等于弹簧力在这个方向分量，每个点在垂直于路径切线方向的受力只等于势能力在此方向上分量。这样弹簧力垂直于路径的分量就被投影掉了，而有用的平行于路径的分量完全保留；势能力在路径方向上的分量也不会再对结构点分布的均匀性产生影响，被保留的它在垂直于路径上的分量将会引导结构点地正确移动。这样优化收敛后结构点就能正确描述真实的MEP，矛盾得到解决。弹簧力常数的设定也比较随意，不会再对结果产生明显影响。但是当平行于路径方向能量变化较快，垂直方向回复力较小的情况，NEB得到的路径容易出现曲折，收敛也较慢，解决这一问题可以引入开关函数，即某点与两个相邻点之间形成的夹角越小，此点就引入更多的弹簧势垂直于路径的分量，使路径不易弯曲而变得光滑，但也会带来一定corner-cutting问题。也可以通过将路径切线定义为每个点指向能量更高的相邻点的方向来解决。

6.7 DNEB方法(Double Nudged Elastic Band)

弹簧势垂直于路径的分量坏处是造成corner-cutting问题，好处是避免路径卷曲。更具体来说，前者是由于它平行于势能梯度方向的那个分量造成的，若只将这个分量投影掉，就可避免corner-cutting问题，而其余分量的力F(DNEB)仍可以避免路径卷曲，这便是DNEB的主要思想。故DNEB与NEB的不同点就是DNEB保留了弹簧势垂直于路径的分量其中的垂直于势能梯度的分量。

DNEB的这个设定却导致结构点不能精确收敛到MEP上。正确的MEP上的点在垂直于路径方向上受势能力一定为0，但是当用了DNEB方法后，若其中某一点处路径是弯曲的，即弹簧力在垂直于路径方向上有分量F'，而且此点势能梯度方向不垂直于此点处路径的切线，即F'不会被完全投影掉，F'力的分量F(DNEB)将继续带着这个点移动，也就是说结构点就不在正确的MEP上了。只有当结构点所处路径恰为直线，即F'为0则不会有此问题。为了解决此问题有人将开关函数加入到DNEB，称为swDNEB，当结果越接近收敛，即垂直于路径的势能力越小的时候，F(DNEB)也越小，以免它使结构点偏离正确MEP。一些研究表明DNEB和swDNEB相比NEB在收敛性（结构点受力最大值随步数降低速度）方面并没有明显提升，DNEB难以收敛到较高精度以内，容易一直震荡。

6.8 String方法

与NEB对力的投影定义一致，但点之间没有弹簧势连接，保持点的间距的方法是每步优化后使这些点在路径上平均分布。

6.9 Simplified String方法

String中计算每个点的切线并投影掉势能力平行于路径的分量的过程也去掉了，所有点之间用三次样条插值来表述路径，每一个点根据实际势能力运动后，在路径上重新均匀分布。优化方法最好结合RK4方法。NEB在点数较小的情况下比Simplified String方法能在更短时间内收敛到更高精度，但点数较多情况下则Simplified String更占优势。

6.10 寻找过渡态的chain-of-state方法

除非势能面对称且结构点数目为奇数，否则不会有结构点恰好落在过渡态。以能量最高的点作为过渡态只是近似的，为了更好地描述过渡态，可以增加结构点数，或者增加局部弹簧力常数，使过渡态附近点更密。根据已得到的点的能量，通过插值方法估算能量最高点是另一个办法。近似的过渡态也可以作为QN法的初猜寻找准确的过渡态。

6.10.1 CI-NEB方法

NEB与String等方法都可以结合Climbing Image方法，它专门考虑到了定位过渡态问题。CI-NEB与NEB的关键区别是能量最高的点受力的定义，在CI-NEB中这个点不会受到相邻点的弹簧力，避免位置被拉离过渡态，而且将此点平行于路径方向的势能力分量的符号反转，促使此点沿着路径往能量升高的方向上爬到过渡态。这个方法只需要很少的点，比如包含初、末态总共5个甚至3个点就能准确定位过渡态，是最有效率的寻找过渡态的方法之一。如果还需要精确描述MEP，可以在此过渡态上使用Stepwise descent方法、最陡下降法、RK4等方法沿势能面下坡走出MEP，整个过程比直接使用很多点的NEB方法能在更短时间内得到更准确的MEP。

6.10.2 ANEBA方法(adaptive nudged elastic band approach)

这个方法也是基于NEB，专用来快速寻找过渡态。一般想得到高精度的过渡态区域，NEB的链子上必须包含很多点，耗费计算时间。而ANEBA方法中链子两端的位置不是固定的，而是不断地将它们移动到离过渡态更近的位置，仅用很少几个点的链子就可以达到同样的精度。具体来说，设链子两端的点分别叫A点和B点（对于第一步就是反应物和产物位置），先照常做NEB，收敛至一定精度后（不需要精度太高），改变A和B的位置为链子中能量最高点相邻的两个点，然后再优化并收敛至一定精度，再如此改变A和B的位置，反复经历这一步骤，最终链子上能量最高点就是精确的过渡态。ANEBA相当于不断增加原先NEB链子的过渡态附近的点数，但实际上点数没有变。有研究表明ANEBA比CI-NEB效率更高，如果结合ANEBA与CI（称CI-ANEBA），即先用ANEBA方法经上述步骤移动几次A、B点，使之聚焦到过渡态附近，再用CI-NEB方法，效率可以进一步提高。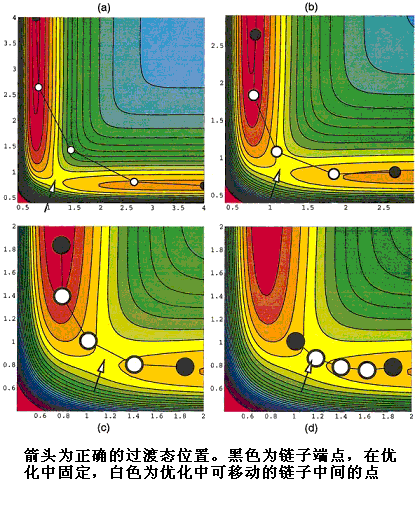

[图16]ANEBA方法示意图

6.11 chain-of-states方法的一些特点

NEB方法的设定只是决定了每一步结构点实际感受到的势能面是怎么构成的，并没有指定优化方法。NEB可以结合一些常见的优化方法，比如最陡下降法、共轭梯度法、quick-min、FIRE、L-BFGS法等（没有线搜索步的全局L-BFGS法效率一般最高），但只能像前述寻找IRC方法一样得到一条路径。实际上很多情况反应的路径不止一条，尤其是势能面复杂的大分子构象转变过程。当NEB结合构象搜索方法，比如分子动力学、蒙特卡罗等方法时，就可以用于寻找多条反应路径。例如有几条反应路径，彼此间都有一定高度的势垒分隔，如果初始给出的路径在第i条附近，优化后只能收敛到第i条路径，若对每个点使用分子动力学方法，设定一定温度，则这些点有机会凭借动能越过势垒到达另外一条路径k附近，随后逐渐降温减小动能，相当于对它们进行最陡下降法优化，就找到了第k条路径，若如此反复多次，有可能找到更多路径。

这类chain-of-states方法的优点还在于易于实现，算法简单，只有能量和其一阶导数是必须要算的，随着体系尺度增大计算量的增加远比基于Hessian矩阵的方法要小。对于大体系储存Hessian并求逆亦是困难的，在某些情况下Hessian矩阵受计算能力制约只能在低水平方法下得到或者无法获得，chain-of-states方法避免了这个问题，很适合用于分子力学研究生物大分子的结构变化路径以及平面波基组下的DFT方法研究固体表面化学反应。此方法也容易并行化，例如可以每个节点负责优化其中一个或几个点，只有计算弹簧力时才需要从另外节点传入相邻结构点坐标，数据通信量小，并行效率高。

6.12 高斯中opt关键字的path=M方法

与chain-of-states方法有一定类似之处，可以在一次计算中获得优化后的过渡态、产物、反应物以及用于描述IRC的中间点结构，总共M个点。此方法须结合QST2或QST3关键字。结合QST2时，除反应物和产物以外剩下的M-2个点在二者冗余内坐标下线性插值产生，结合QST3则是剩下的M-3个点在反应物与过渡态、过渡态与产物之间插值产生。之后迭代的每一步主要分为以下几个步骤：(1)初始输入的反应物、产物通过RFO法向最优构型优化。(2)能量最高的点q(k)（此点在第一步确定）通过EF法向过渡态优化，并设一段圆弧通过q(k-1)、q(k)、q(k+1)，此圆弧在q(i)处的切线作为EF方法选择所跟踪的本征向量的引导，类似于STQN步。(3)其余的点执行微迭代步骤（迭代内的迭代），其中包含类似于GS法的球面优化步骤以及调整间距步骤。可参考图14，优化其中任意点q(i)前，首先获得经过q(i-1)、q(i)并与q(i-1)的梯度相切的圆弧或曲线，将其在q(i)处的切线定义为T(i)，然后定义一个在q(i)处法线与T(i)平行、经过q(i-1)与q(i)的球面，使q(i)限制在此球面上优化。然后在这些点依次相连的路径上调整这些点的间距至平均，之后重复微迭代直至每一步力和位移都已收敛，或者有任何点位移超过了置信半径。(4)检查力和位移是否都已收敛至标准。这个方法看上去比单独优化反应物、产物、过渡态并计算IRC省时间，但是实际用起来并不好用，容易出错。

6.13 CPK方法(Conjugate Peak Refinement)

在某种意义上称为动态的chain-of-states方法。每条链子只含一个可动点，链子数由最初的一条开始不断增加，对MEP的描述也越来越精确。CPK中的第一步类似LST，在连接反应物和产物的直线中找到能量最高点（称为Peak），然后沿着共轭方向优化得到中间点，对中间点与反应物、中间点与产物分别再做上述步骤，先找到最大点再共轭优化，如此反复直到收敛。最后将反应物、产物以及执行CPK过程中所有优化后的点相连，就得到了近似的反应路径。CPK方法所得的反应路径可以经过很多过渡态，很适合寻找一些涉及到复杂结构重排、包含甚至上百个过渡态的构象变化路径，如蛋白质局部折叠/去折叠过程。CPK方法缺点是实现起来相对复杂，定位过渡态较为费时。

[图17]CPK方法示意图