用NBO计算原子轨道杂化后的能量变化
用NBO计算原子轨道杂化后的能量变化
Use NBO to calculate energy change after hybridization of atomic orbitals
今天在思想家公社1群里有人问这种图里面的能量怎么得到

可以通过做价键计算来得到,但是比较麻烦。一种简单粗略的得到方法是用NBO。
用过NBO的人都知道,NBO分析可以直接给出NAO和NBO的能量。比如计算甲烷,有这样的输出
NAO Atom No lang Type(AO) Occupancy Energy
----------------------------------------------------------
1 C 1 S Cor( 1S) 1.99963 -11.07292
2 C 1 S Val( 2S) 1.16479 -0.30941
3 C 1 S Ryd( 3S) 0.00000 1.31567
4 C 1 S Ryd( 4S) 0.00000 4.60142
5 C 1 px Val( 2p) 1.23058 -0.06639
6 C 1 px Ryd( 3p) 0.00000 0.76994
7 C 1 py Val( 2p) 1.23058 -0.06639
8 C 1 py Ryd( 3p) 0.00000 0.76994
9 C 1 pz Val( 2p) 1.23058 -0.06639
10 C 1 pz Ryd( 3p) 0.00000 0.76994
...略
BD型NBO是由成键的两个原子通过其NHO组合而成的,NHO就是原子用于成键时所用的杂化轨道,其能量正是绘制上图中杂化轨道位置所需的值。NHO的能量在NBO程序里没有直接输出,但可以用FNHO关键词来输出NHO构成的Fock矩阵,对角元便是各个NHO的能量。Gaussian自带的NBO 3.1支持这个关键词,使用pop=nboread,末尾空一行写$NBO FNHO $END即可。
对甲烷,得到的FNHO矩阵为
NHO 1 2 3 4 5 6 7 8
---------- ------- ------- ------- ------- ------- ------- ------- -------
1. C 1( H 2) -0.1212 -0.6891 -0.0628 -0.0683 -0.0628 -0.0683 -0.0628 -0.0683
2. H 2( C 1) -0.6891 0.1754 -0.0683 -0.0684 -0.0683 -0.0684 -0.0683 -0.0684
3. C 1( H 3) -0.0628 -0.0683 -0.1212 -0.6891 -0.0628 -0.0683 -0.0628 -0.0683
4. H 3( C 1) -0.0683 -0.0684 -0.6891 0.1754 -0.0683 -0.0684 -0.0683 -0.0684
5. C 1( H 4) -0.0628 -0.0683 -0.0628 -0.0683 -0.1212 -0.6891 -0.0628 -0.0683
6. H 4( C 1) -0.0683 -0.0684 -0.0683 -0.0684 -0.6891 0.1754 -0.0683 -0.0684
7. C 1( H 5) -0.0628 -0.0683 -0.0628 -0.0683 -0.0628 -0.0683 -0.1212 -0.6891
8. H 5( C 1) -0.0683 -0.0684 -0.0683 -0.0684 -0.0683 -0.0684 -0.6891 0.1754
...略
第一个对角元,即是C1和H2成键时C的杂化轨道的能量,即-0.1212 a.u.。非对角元则体现NHO之间的耦合,也可以用E2的方式基于NHO能量和这些非对角元来估算NHO间的二阶稳定化能。
在NBO的输出部分,可以看到各个杂化轨道是怎么组成的,比如
1. (1.99932) BD ( 1) C 1 - H 2
( 60.79%) 0.7797* C 1 s( 25.00%)p 3.00( 74.88%)d 0.00( 0.12%)
0.0001 0.5000 0.0000 0.0000 0.4996
0.0000 0.4996 0.0000 0.4996 0.0000
0.0198 0.0198 0.0198 0.0000 0.0000
( 39.21%) 0.6262* H 2 s(100.00%)
1.0000 -0.0006
...
这里显示,形成C-H键时C的NHO的组成是s( 25.00%)p 3.00( 74.88%),即标准的sp3杂化。
我们得到的NHO的能量是合理的,因为如前所示,C的s(val)轨道能量是-0.30941 a.u.,p(val)轨道能量是-0.06639 a.u.,按照1:3杂化,NHO的能量原理上为-0.30941/4-0.06639*3/4=-0.127145 a.u.,和-0.1212 a.u.很接近(不完全相同是因为分子环境里NHO的构成并非精确sp3,而且还有周围化学环境对能量产生影响,等等)。
对NHO图形感兴趣的话可以用此文方法观看:《使用Multiwfn绘制NBO及相关轨道》(http://sobereva.com/134)。C的那个NHO图像如下,可见确实是明显的s和p轨道混合产生的
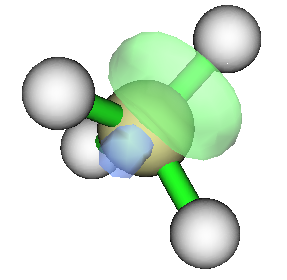
最后提醒一下,NBO里的NHO和结构化学里说的杂化轨道有一定区别。比如甲醛,结构化学里说C用于和周围三个原子形成sigma键用的三个sp2轨道构成是完全相同的,不做区分。但是NBO程序里,这个碳原子构成C-H和C-O sigma型NBO用的NHO是不同的,且能量相差甚巨。