Multiwfn的格点数据平移功能介绍
Multiwfn的格点数据平移功能介绍
Introduction to grid data translation function in Multiwfn
文/Sobereva@北京科音 2025-Nov-19
1 前言
很多人在对周期性体系绘制三维函数(如电子密度差)的等值面时,容易遇到一个情况是发现感兴趣的等值面在晶胞的边缘,导致等值面被截断,无法观看完整。虽然VMD程序在显示格点数据等值面的时候可以要求把周期镜像显示出来,从而试图让位于晶胞边缘的等值面看起来完整,但等值面在晶胞边界的位置会不连贯,有个突变,因而还是不好看。还有一个解决方法是先用《Multiwfn中非常实用的几何操作和坐标变换功能介绍》(http://sobereva.com/610)里提供的功能令晶胞进行平移使得感兴趣的区域在盒子中央,然后再重新计算格点数据,但这个过程不仅麻烦而且还花费重算一次的时间。
为了完美地解决以上问题,在2025-Nov-19更新的Multiwfn中增加了一个新功能,可以令格点数据连带着原子坐标在盒子的第1、2、3个轴上分别平移特定百分比,从而将感兴趣的等值面移到便于观察的地方,整个过程瞬间完成。下面就通过两个实际例子演示一下。Multiwfn可以在官网http://sobereva.com/multiwfn免费下载,不了解Multiwfn者建议看《Multiwfn FAQ》(http://sobereva.com/452)。记录格点数据最常用的格式是cube,不了解的话建议看《Gaussian型cube文件简介及读、写方法和简单应用》(http://sobereva.com/125)。
2 实例
北京科音CP2K第一性原理计算培训班(http://www.keinsci.com/KFP)里我讲CP2K做水合电子的AIMD模拟的幻灯片中,给了三个时刻的自旋密度等值面的图片,如下所示。由图可见从2000 fs时开始形成水合电子,到了2100 fs时水合电子已经完全形成。然而2100 fs时的等值面在盒子最边上,看起来很不舒服。这个问题靠前述的Multiwfn的格点数据平移功能即可解决。
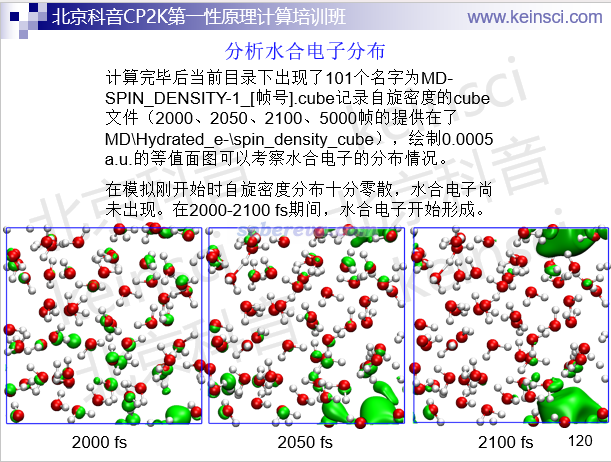
2100 fs时刻CP2K产生的这个体系的自旋密度的cube文件MD-SPIN_DENSITY-1_2100.cube在http://sobereva.com/attach/754/file.rar中。我们先看一下等值面图,用VMD、VESTA、Multiwfn等观看都可以。此例用Multiwfn载入cube文件后,进入主功能0,把等值面数值设为0.001,并且点击show data range复选框要求显示格点数据盒子边框后就可以看到下图
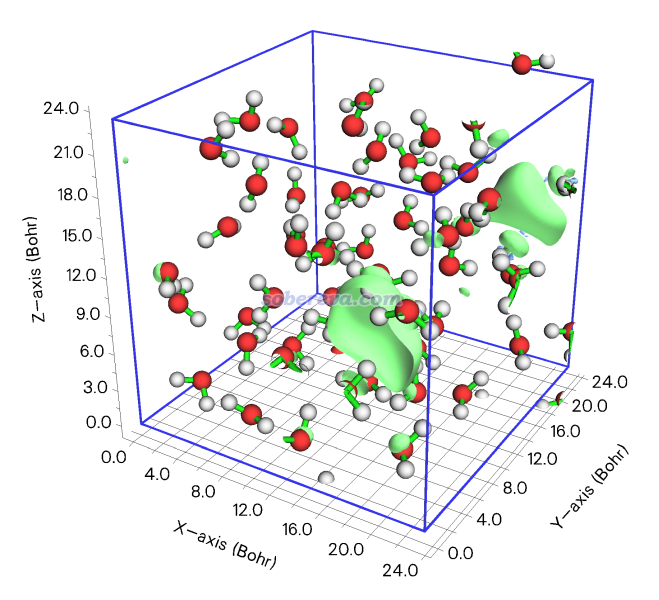
显然,为了让等值面位于盒子中央便于观看,应该对体系在第1个轴(当前对应X轴)的负方向平移30%左右;在第2个轴(当前对应Y轴)的正方向平移约50%;在第3个轴(当前对应Z轴)上用不着平移。
关闭图形窗口回到Multiwfn主菜单,依次输入
13 //处理内存中的格点数据的功能
19 //平移格点数据
-0.3 //在第1个轴负方向平移30%
0.5 //在第2个轴正方向平移50%
[回车] //不在第3个轴方向上平移
此时屏幕上看到如下提示,显示了在各个方向上平移了多少个格点,以及平移矢量。注意这里都是按正值显示(由于周期性,前面输入-0.3等同于输入了0.7)。
Translate along the 1st axis by 62 grids
Translate along the 2nd axis by 45 grids
Translate along the 3rd axis by 0 grids
Translation vector: 8.630404 6.264003 0.000000 Angstrom
当前程序检测到在平移后有些原子露在了盒子外面,问你是否把它们卷到盒子里,这里输入y要求卷入。
现在格点数据就处理好了。可以选择选项0把格点数据导出为新的.cub文件,也可以直接选选项-2观看等值面,现在看到的图如下。可见等值面已完全在盒子中央了,非常容易考察水合电子的形态。
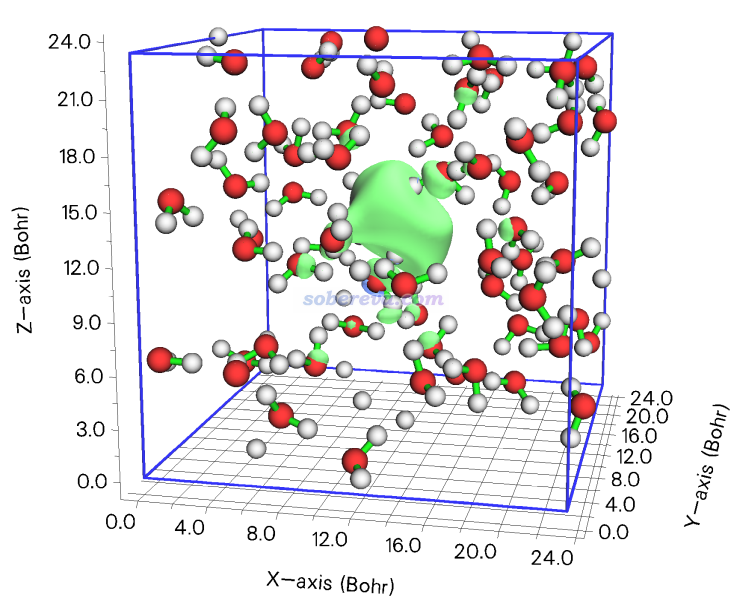
3 注意事项
此功能对任何函数的格点数据都可以用。格点数据可以是从cube、CHGCAR等Multiwfn支持的记录格点数据的文件中读取的,也可以是Multiwfn的主功能5等功能基于波函数文件直接计算出来并存在内存中的。
本文介绍的功能对于盒子是非正交的情况也可以照常用,平移的方向对应于实际三个轴的方向,只不过Multiwfn目前无法正确显示这种情况的等值面,应当用VMD、VESTA等程序显示。
前面的例子中,格点数据对应的盒子(即均匀分布的格点所处的范围)和做周期性第一性原理计算对应的盒子(对晶体体系来说也相当于晶胞)是完全一致的。如果格点数据的盒子范围和周期性计算用的盒子范围不对应,比如计算格点数据的区域只是整个体系中的一小块,那么使用本文的功能就没任何意义。
如果你的体系本来就没周期性,本文的功能虽然也能使用,但并没有任何实际意义。
如果本文的功能给你的研究带来了便利,发表文章时请引用Multiwfn启动时提示的原文。