使用Multiwfn基于Hirshfeld-I划分计算特定类型电子在各个原子上的分布量
使用Multiwfn基于Hirshfeld-I划分计算特定类型电子在各个原子上的分布量
Using Multiwfn to calculate the distribution of specific types of electrons on each atom based on Hirshfeld-I partitioning
文/Sobereva@北京科音 2024-Jan-26
在《18碳环等电子体B6N6C6独特的芳香性:揭示碳原子桥联硼-氮对电子离域的关键影响》(http://sobereva.com/696)中提到,笔者在Inorg. Chem., 62, 19986 (2023)一文考察B6C6N6分子的电荷分布时,专门计算了此分子的平面内π轨道、平面外π轨道、σ轨道和内核轨道上的电子是怎么分布在各个原子上的。原子空间定义的方法不唯一,此文用的是流行的Hirshfeld-I原子空间划分,这种方式划分的原子空间物理意义较强,可以较合理体现外环境导致的原子空间收缩和膨胀。这种分析方法对于读者研究很多其它体系也很有益处。本文就演示一下怎么用Multiwfn实现这种计算,以计算B6C6N6的平面内π电子(π-in)的分布为例。由于这个计算需要充分利用Multiwfn的灵活性,牵扯一些细节,这是为什么我专门写个文章来具体说明。
上述文章考察的B6N6C6的波函数文件是http://sobereva.com/attach/697/B6C6N6_OS.rar,解压后是B6C6N6_OS.fchk,是由Gaussian 16在wB97XD/def2-TZVP级别下以对称破缺方式计算得到的。本文例子用的Multiwfn是2024-Jan-21更新的版本。Multiwfn可以在http://sobereva.com/multiwfn免费下载,不了解者看《Multiwfn FAQ》(http://sobereva.com/452)。
启动Multiwfn,载入B6C6N6_OS.fchk。首先要做的是构造Hirshfeld-I原子空间,把Multiwfn的examples目录下的atmrad子目录挪到当前目录下,这是因为此目录下有各种元素不同价态的径向电子密度信息,在构造Hirshfeld-I原子空间时要用到(若缺乏计算机常识不了解什么叫“当前目录”,看http://sobereva.com/237)。然后在Multiwfn里依次输入
15 //模糊空间分析
-1 //选择原子空间
1 //开始构造Hirshfeld-I原子空间
很快就构造完了。Hirshfeld-I原子空间权重数据现已被储存在了内存里,输入0返回主菜单。
因为我们要考察π-in分子轨道上的电子分布,故接下来需要把这类轨道以外的分子轨道的占据数都清零。可以按照《使用Multiwfn观看分子轨道》(http://sobereva.com/269)说的,在Multiwfn主功能0里一个一个观看占据轨道的图形判断,把π-in轨道的序号都记录下来,最终找到的序号如下。注意当前是对称破缺计算,因此两种自旋要分别考察。
Alpha自旋的π-in占据轨道:38,41,42,45,46,48,50,53,54
Beta自旋的π-in占据轨道:596,599,600,603,604,606,608,611,612(注意beta轨道序号在Multiwfn中的记录规则,在http://sobereva.com/269专门说了)
在Multiwfn里接着输入
6 //修改波函数
26 //修改轨道占据数
0 //选择所有轨道
0 //把所有轨道占据数清零
38,41,42,45,46,48,50,53,54,596,599,600,603,604,606,608,611,612 //所有π-in轨道序号
1 //占据数还原为原本的1.0
q //返回
-1 //返回主菜单
现在就可以开始正式计算了。在Multiwfn里接着输入
15 //模糊空间分析。进入后从选项-1的文字上可以看到当前的原子空间仍是Hirshfeld-I
1 //对特定实空间函数在各个原子空间中积分
1 //被积函数是电子密度。显然当前对应的是π-in电子密度
马上看到如下结果
Atomic space Value % of sum % of sum abs
1(B ) 0.64940465 3.607804 3.607804
2(C ) 1.00713759 5.595209 5.595209
3(N ) 1.34345778 7.463655 7.463655
4(B ) 0.64926116 3.607007 3.607007
5(C ) 1.00733834 5.596325 5.596325
6(N ) 1.34338216 7.463235 7.463235
7(B ) 0.64944181 3.608010 3.608010
8(C ) 1.00710182 5.595011 5.595011
9(N ) 1.34348431 7.463802 7.463802
10(B ) 0.64924542 3.606919 3.606919
11(C ) 1.00734233 5.596347 5.596347
12(N ) 1.34339152 7.463287 7.463287
13(B ) 0.64942036 3.607891 3.607891
14(C ) 1.00713369 5.595188 5.595188
15(N ) 1.34344824 7.463602 7.463602
16(B ) 0.64928283 3.607127 3.607127
17(C ) 1.00730639 5.596147 5.596147
18(N ) 1.34341808 7.463434 7.463434
Summing up above values: 17.99999847
Summing up absolute value of above values: 17.99999847
如上可见,B、C、N原子的π-in电子数分别是0.649、1.007、1.343,和如下所示的Inorg. Chem., 62, 19986 (2023)中的表2中的数据完全一致。
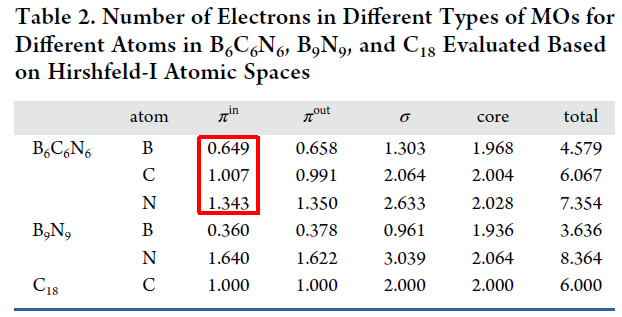
最后再提醒一下,必须按以上说明先产生Hirshfeld-I原子空间、修改轨道占据数,最后再在Hirshfeld-I原子空间里积分,而不能先修改轨道占据数然后再进入子功能15产生Hirshfeld-I原子空间并做积分。因为修改轨道占据数之后,此时的电子密度函数就不再是总电子密度了,而Hirshfeld-I原子空间在构造时用到的电子密度函数必须对应总电子密度。