优化长程校正泛函w参数的简便工具optDFTw
注:在北京科音高级量子化学培训班(http://www.keinsci.com/KAQC)中专门有一节“DFT泛函的调控”,其中笔者用了50多页幻灯片对DFT泛函的调控做极尽全面系统和深入的讲解,信息量是本文的5倍以上,十分推荐对这部分内容感兴趣的读者参加!
优化长程校正泛函w参数的简便工具optDFTw
OptDFTw: A utility for optimizing the w parameters of long-range correction functionals
文/Sobereva @北京科音
First release: 2016-Sep-20 Last update: 2024-Nov-12
1 简介
这几年优化长程校正泛函的w参数(其实是ω,为打字方便就写成w)的做法很火,文章接连不断,有兴趣者可以看看钟成等人的综述《最优化“调控”区间分离密度泛函理论的研究进展》(DOI: 10.3866/PKU.WHXB201605301)。对w进行调节的一种较好方法是使当前w下计算的HOMO轨道能量尽可能接近电离能。这么做的物理思想是对于精确的交换相关泛函,HOMO能量精确等于电离能,即Koopmans定理完全满足。这么调节w之后,长程校正泛函可以很好地计算激发能、(超)极化率、fundamental gap、单-三重态激发态能量差等问题(但也并非万能,比如有大小一致性问题、JPCB,119,1202发现有的体系的超极化率即便w经过优化还是算不好)。w对体系依赖性大,针对一个体系优化的w,对于另一个体系就往往很不适合,所以对每个被计算的体系都需要优化w,导致比普通泛函计算要多花不少代价。
这里提供笔者写的极其简单易用的优化w参数的工具optDFTw,以及附带的对w做扫描的工具scanDFTw。
用于Gaussian09版的下载地址:http://sobereva.com/soft/optDFTw_1.0_g09.zip
用于Gaussian16版的下载地址:http://sobereva.com/soft/optDFTw_1.0_g16.zip
其中.exe的是Windows版可执行文件,没后缀的是Linux版可执行文件。
若文章使用这两个程序,请引用:Tian Lu, optDFTw program v1.0, webpage: http://sobereva.com/346。
这两个程序目前只支持Gaussian程序。只支持中性体系的计算。Windows下运行之前需要在系统中添加GAUSS_EXEDIR环境变量使之指向g09.exe或g16.exe所在目录,并且在PATH环境变量里也添加这个目录,使得能通过命令行方式顺利调用Gaussian。
2 optDFTw程序
此程序涉及两个量,J和J^2,都是衡量N电子态以及N+1电子态时HOMO能量与电离能的偏差之和。注意J^2不是J直接取平方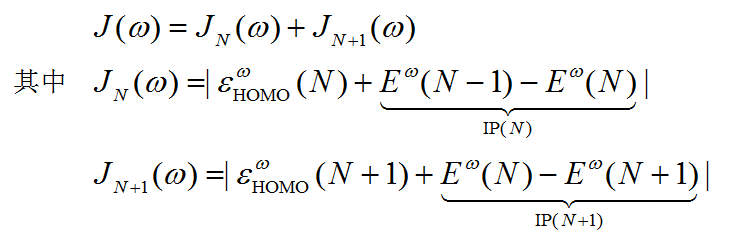
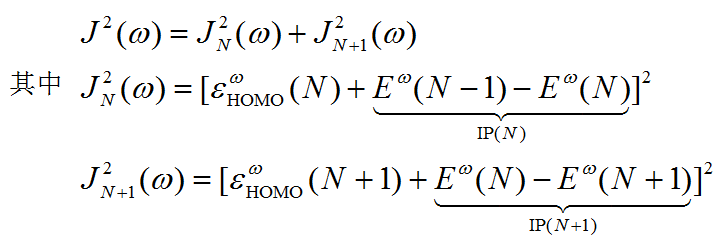
令J或J^2函数最小化就找到了最优的w。由于J^2对w更敏感,所以optDFTw优化的是J^2。这个程序是基于Brent算法来最小化J^2的。优化过程是迭代过程,令w收敛到0.0001就已经足够精确了,这一般只需要十来圈,如果收敛到0.001一般也就<=十圈。
使用optDFTw程序前首先要编辑一个Gaussian的长程校正泛函的单点任务文件作为模板,存到当前目录下template.gjf中,比如
%mem=60GB
%nproc=16
# LC-wPBE/6-311+G**
test
0 1
C 0.00000000 0.00000000 -0.52710800
H 0.00000000 0.93885600 -1.11413900
H 0.00000000 -0.93885600 -1.11413900
O 0.00000000 0.00000000 0.67386600
基组可以是混合基组,照常写即可。泛函可以是比如LC-wPBE、LC-BLYP等标准长程校正泛函,wB97、wB97XD等近程HF成分不为0的泛函可能也能用但结果未必可靠(数据自行负责)。之后在optDFTw运行过程中,就会基于这个文件产生对应不同电子数的N.gjf、N-1.gjf、N+1.gjf,并调用Gaussian进行运算,然后从输出文件中读取计算J^2所需的HOMO轨道能量和体系总能量。在Gaussian中用长程校正泛函计算时,将IOp 3/107和3/108都设为MMMMM00000就相当于用了w参数为MMMMM/10000的范围分离泛函,所以每一步optDFTw都是靠这俩IOp来实现不同w下计算的。
在template.gjf准备好后直接启动optDFTw就可以进行对w的优化。Brent优化算法需要给定初始的w范围以及初猜,给得越合适越可能用较少步数收敛,范围一定要能够把实际的w值囊括在此范围中。默认的w下限是0.05(不能写0,否则Gaussian没法运行),默认上限是0.6(一般足够大了),默认的w收敛限是0.0001,默认的初猜值是上下限的中间值。如果要自己设这些参数,需要以命令行方式运行,即:
下面是实际运行的输出例子(随便选的分子,和上面的示例输入文件不对应),可见每一轮对N、N+1、N-1体系分别算一次单点。经过14轮,最终优化的w是0.373547 Bohr^-1,之后在Gaussian中使用此范围分离泛函时就应当写IOp(3/107=0373500000,3/108=0373500000)了。
Lower limit: 0.050 Upper limit: 0.600 Init w: 0.325 Tol: 0.00010
The initial point:
Running: g09 N.gjf N.out
Running: g09 N-1.gjf N-1.out
Running: g09 N+1.gjf N+1.out
w: 0.325000 J: 0.0158995406 J^2: 0.0001837031
Iteration: 1
Running: g09 N.gjf N.out
Running: g09 N-1.gjf N-1.out
Running: g09 N+1.gjf N+1.out
w: 0.430041 J: 0.0179941437 J^2: 0.0001839521
Iteration: 2
Running: g09 N.gjf N.out
Running: g09 N-1.gjf N-1.out
Running: g09 N+1.gjf N+1.out
w: 0.219959 J: 0.0661930709 J^2: 0.0026101120
...略
Iteration: 13
Running: g09 N.gjf N.out
Running: g09 N-1.gjf N-1.out
Running: g09 N+1.gjf N+1.out
w: 0.373584 J: 0.0024404394 J^2: 0.0000039539
Iteration: 14
Converged!
The final w: 0.373547 Bohr^-1 J^2: 0.0000039466
3 scanDFTw程序
scanDFTw程序是在指定范围内按照指定步长对w进行扫描,对每个w会输出J和J^2值。运行前需要以和optDFTw同样的方式编写template.gjf放到当前目录下。默认从0.05扫到1.0,步长是0.05。如果自行调节设定,用命令行方式运行:iverb默认为0,如果想同时输出每个w值的HOMO轨道能量和体系总能量则设为1。比如scanDFTw 0.3 0.5 0.02 1。下面是输出例子,可见最优的w在w=0.35附近。
w: 0.050000 J: 0.20647538 J^2: 0.02246148
w: 0.100000 J: 0.15601700 J^2: 0.01319407
w: 0.150000 J: 0.11338736 J^2: 0.00721878
w: 0.200000 J: 0.07836289 J^2: 0.00359102
w: 0.250000 J: 0.04967293 J^2: 0.00151705
w: 0.300000 J: 0.02609101 J^2: 0.00045375
w: 0.350000 J: 0.00661196 J^2: 0.00004245
w: 0.400000 J: 0.00958336 J^2: 0.00004770
w: 0.450000 J: 0.02312111 J^2: 0.00031436
w: 0.500000 J: 0.03450162 J^2: 0.00073904
w: 0.550000 J: 0.04413207 J^2: 0.00125304
w: 0.600000 J: 0.05233264 J^2: 0.00181038
w: 0.650000 J: 0.05936051 J^2: 0.00238061
w: 0.700000 J: 0.06541519 J^2: 0.00294496
w: 0.750000 J: 0.07066110 J^2: 0.00349063
w: 0.800000 J: 0.07522949 J^2: 0.00400930
w: 0.850000 J: 0.07921135 J^2: 0.00449682
w: 0.900000 J: 0.08271471 J^2: 0.00495013
w: 0.950000 J: 0.08577732 J^2: 0.00536856
若optDFTw或scanDFTw调用Gaussian计算时意外中断,显然是Gaussian计算出错,自行打开屏幕上提示的Gaussian的out文件,根据末尾的报错信息结合Gaussian使用常识自行判断怎么解决,不要在群里或论坛里问我。>90%的概率是SCF不收敛,参考《解决SCF不收敛问题的方法》(http://sobereva.com/61)试图在模板文件里加帮助收敛的关键词,或者尝试其它基组、几何结构等方式解决。也可能是净电荷/自旋多重度设置不对、Gaussian运行环境有问题、内存不够等原因,自行看报错提示判断。
4 溶剂效应的考虑
为避免一些人犯错,这里特别一提,如果你要在之后的研究中考虑隐式溶剂模型,那么w调控的时候不要直接带着溶剂模型。参考北京科音高级量子化学培训班(http://www.keinsci.com/KAQC)下面这页ppt。在培训里有具体做法的专门的介绍



