谈谈分子半径的计算和分子形状的描述
文/Sobereva @北京科音
First release:2013-Jun-7 Last update:2019-Oct-21
1 球形模型
用球形模型,相当于讨论怎么计算分子的半径。首先要认识到,分子半径不是一个可观测量,在计算方法上也不可能有唯一的定义,因此“怎么计算分子半径”这个问题本身就是不严格的。这段话和笔者在《谈谈分子体积的计算》(http://sobereva.com/102)当中文首说的话几乎如出一辙。对于半径、体积这类没有唯一定义的问题,应该先想清楚计算原理是什么,不要盲目计算。
谈到分子半径,这就自然已经假设了分子必须能较好作为球形来描述,如甲烷、球蛋白,至少也不能偏离球型太远。如果偏离球形很远,例如分子是大平面,像是卟啉或多环芳烃,或者是长链,如直链烷烃,那么就不可能靠球形模型来描述,也因此讨论半径对于这种问题是无意义的。
计算分子半径的做法有很多,下文将列举一些,但肯定还有不少方法本文中没有提及。
1 寻找分子内相距最远的两个原子距离,然后加上相应两个原子的范德华半径,得到分子直径,除以2即是分子半径。
2 寻找与分子几何中心最远的原子距离,加上其范德华半径,得到分子半径。(更严格地说,应该是找出加上相应范德华半径之后几何中心离哪个原子最远,不过本文就不考虑这点了)
上面这两种方法计算起来比较容易,特别是方法1,直接在分子可视化工具里测量一下就行,不过原子很多的时候测量起来可能困难些。这两种方法的计算在Multiwfn程序(http://sobereva.com/multiwfn)里可以直接实现。这里以水分子为例。首先载入Multiwfn支持的含有分子结构信息的文件,如.pdb、.xyz、.mol等都可以,然后进入主功能100,然后选21,再输入all。屏幕上马上出现基于分子结构计算出的各种信息,其中可看到几何中心坐标
Geometry center (X/Y/Z): 0.00000000 0.00000000 -0.27838535 Angstrom
下面会看到
Maximum distance is 1.517906 Angstrom, between atom 2(H ) and 3(H )
代表2H和3H距离最远,相距1.52埃。H的bondi定义的范德华半径为1.2埃(见JCP,68,441(1964)),因此按照方法1计算的分子半径即为(1.52+2*1.2)/2=1.96埃。
从输出信息中还看到
The atom farthest to geometry center is 2(H ) Dist: 0.784570 Angstrom
说明与几何中心距离最远的是2H且相距0.784埃,加上H的范德华半径,0.784+1.2=1.984埃即是方法2算得的分子半径。
如果用的是2018-Jun-6之后更新的Multiwfn,以方法1计算半径还有更省事的办法,即进入主功能100的子功能21之后,输入size,屏幕上直接就会输出Radius of the system: 1.959 Angstrom这样的信息。
可以利用VMD程序来画出球形,来直观地比较分子结构和圆球的定义。将水分子结构文件载入VMD,在控制台输入以下命令,来绘制一个透明的半径是1.984埃的圆球,其球心在几何中心(上述过程中Multiwfn的输出信息中已包含了几何中心位置)。draw material Transparent
draw sphere { 0 0 -0.278 } radius 1.984 resolution 30
color Display Background white
然后在Graphics - Representation里把显示方式改成CPK,最后效果如下,可见这个圆球比较好地包裹了整个水分子。
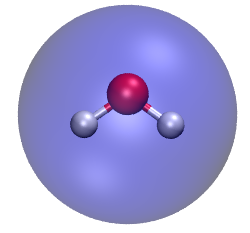
对于凝聚相体系,由于分子间互相挤压或者存在诸如氢键这种相互作用,原子的范德华半径会在一定程度上被穿透,所以,上述方法估算的分子半径可能有所高估。因此,加上原子范德华半径时可以考虑给范德华半径乘个<1的刻度因子来体现这个效应。
上述两种方法结果往往相差不大,由于计算简便,适合计算很大体系的半径,如蛋白质。
3 寻找分子表面最远的两个点的距离作为分子直径,除以2即是分子半径。分子表面的定义很多,见《谈谈分子体积的计算》的讨论,不同的表面适用于不同情况,例如Bader建议以电子密度0.001/0.002 a.u.的等值面分别作为气相/凝聚相时的范德华表面。这种方法类似方法1,但更严格、准确。
4 寻找分子几何中心距离分子表面最远处的距离作为分子半径。这个方法类似方法2,但比它更严格、准确。
方法3、4可以通过Multiwfn的定量分子表面分析功能实现。做法是启动Multiwfn后,载入相应体系的含有波函数信息的文件(如.wfn、.fch、.molden),然后进入主功能12,选0开始构建分子表面并进行表面性质的分析(默认是0.001 a.u.等值面作为分子表面,可用选项1修改)。然后在后处理菜单中选10,再输入g,屏幕上就会输出分子表面上距离几何中心最近和最远的距离;如果输入f,程序会计算出分子表面上最远两个点的距离,以及这两个点及其中点的坐标,之后可以像前例一样通过中点位置以及最远距离的一半作为半径在VMD中画出透明的球面。
(注:主功能12默认分析的是分子表面上的静电势,而静电势计算对大体系会比较慢。由于我们的目的只是得到表面顶点而非分析表面的性质,所以可以进入主功能12之后先选择2设置被映射的函数,再选-1,然后选0开始分析。这里0代表考察的是用户自定义函数,这个函数默认情况下是个常数,没有任何计算耗时。)
对于水分子,在0.001 a.u.等值面作为范德华表面的情况下,利用Multiwfn程序得出的方法3定义的半径为1.99埃,方法4定义的半径为2.15埃。如果使用0.002 a.u.等值面当做范德华表面,则方法3、4定义的分子半径将缩小一些,分别为1.85埃和2.02埃。
由于方法3、4都依赖于电子密度信息,所以用不同理论方法、基组计算波函数文件,所得半径结果会有些许差异。
对于很大体系,利用方法3、4来计算半径总耗时会颇长,所以此时还是建议用方法1、2,尽管原则上精度会差一些,但是对于体系这么大的情况,那点精度的损失是完全可以忽略的,更何况分子半径的定义本身就是含糊的。
5 计算分子体积V,然后根据V=4/3*pi*r^3来解出分子半径r。例如水分子,电子密度0.002 a.u.的等值面内的体积约为20.92埃^3,因此r=1.71埃。如果用0.001a.u.等值面当做范德华表面,则体积约为26.36埃^3,因此r=1.85埃。通过电子密度等值面定义的体积可以利用Multiwfn程序得到,见《谈谈分子体积的计算》。
之所以我们用这个方法算得的半径比前述的方法略小,这并不难理解,因为此方法相当于把任意形状的分子给攒成了理想球形,所以看起来当然变小了。如果分子偏离球形更多,那么此方法所得半径将小得更多。
6 假定分子之间是无缝隙地堆积起来的,根据物质的密度推出分子体积和半径。可用先用此公式解出分子体积:M/(V*10^-27*NA)=rho,即V=M/rho/6.02*10000,其中M是分子量,rho是密度(g/L)。例如水的rho=1000g/L,M=18.0,故V=29.9埃^3。将分子当成理想球形解得的分子半径即为r=1.92埃。
7 对于AHn类分子(如H2O、NH3、CH4等),将重原子作为球中心,逐渐增加半径,当半径增大到一定值时球内电子密度恰包含了体系内98%的电子密度时,将这个半径作为分子半径。这个定义是JCP, 56, 4419(1972)提出的,如今很少有人用,算起来也不方便,也不是很普适。此文算出的水的半径是1.67埃。
除上述这些,分子半径/直径还可以根据某些实验来给出。比如可以根据能否通过指定孔径的分子筛来确定分子直径。这和动力学直径关系密切,用Multiwfn可以容易地算出动力学直径,见《使用Multiwfn计算分子的动力学直径》(http://sobereva.com/503)。顺带一提,Multiwfn还有计算分子孔洞直径的功能,见《使用Multiwfn计算分子和晶体中孔洞的直径》(http://sobereva.com/643)。
对于聚合物,也包括蛋白质等体系,经常讨论回转半径用来讨论分子构象延伸的广度。比如在一个蛋白去折叠过程中蛋白质链会伸展得越来越广,回转半径也因此逐渐增大。但有人以为回转半径可以当成分子半径,这是明显错误的。例如,我们用一个酪氨酸激酶作为示例,总共有1806个原子,我们用前述方法2得到的半径是30.638埃,而回转半径是16.842埃。以几何中心作为球心,用方法2所得半径和回转半径绘制的球分别以蓝色和黄色表示,所得图像如下所示
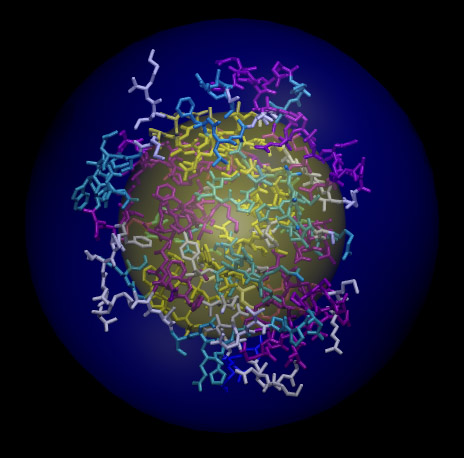
可见回转半径根本没有包住整个体系。所以说,回转半径适合衡量结构的延展广度,但不适合作为分子半径的定义。回转半径也可以通过Multiwfn得到,依然是进入主功能100里的功能21,输入all之后输出的信息里就有整个体系的回转半径,即Radius of gyration:后面的数值。
2 圆片/圆柱模型
对于大平面分子,我们描述其分子形状显然就不适合再用圆球模型了。诸如卟啉这样的分子,我们适合使用扁圆片模型来描述它的形状。圆片的厚度可以简单定义为碳原子范德华半径的二倍,而圆片的半径可以直接使用前述的方法1~4来得到。
对于长链体系,其形状适合用圆柱模型来表示。我们可以沿用前述的方法1~4来得到圆柱的长,而圆柱的半径需要根据实际结构来判断。
一种更为严格、自动化的确定圆柱参数的方法是不断调整圆柱的参数,使得圆柱能够包围所有原子且圆柱的尺寸最小。这个方法可以借住CYL程序来完成。此程序可以在这里免费下载到Linux和Mac OS X版:http://petitjeanmichel.free.fr/itoweb.petitjean.freeware.html
CYL程序下载后直接用诸如./bin.CYL.1.linux64.intel命令运行即可,然后输入输入文件的路径。输入文件格式类似这样:
63 0 0 0 //63代表有63个点。后面的三个零不用管,一般都需要写。
-12.235 -1.599 -0.445 //各个点的XYZ坐标,对于本文的情况也就是各个原子坐标
-10.905 -1.894 -0.414
-9.920 -0.847 -0.263
-10.369 0.509 -0.148
-11.788 0.778 -0.186
-12.685 -0.238 -0.329
-8.546 -1.127 -0.228
...略
对于点比较多的情况,计算要花不少时间。算完后屏幕上会看到诸如
Axis : 0.996020E+00 0.491685E-01 0.743408E-01
Center: 0.529569E+00 0.669861E+00 0.659797E+00
Radius : 0.305604E+01
Half-height: 0.143397E+02
Axis就是圆柱的轴的矢量,Center是圆柱中心,Radius是圆柱半径,Half-height是圆柱长度的一半。利用这样的信息,我们可以将圆柱的图形画出来,以便和分子结构相比较。我们使用VMD程序内建的绘图命令来画图。
在启动VMD后,先载入分子结构文件,然后在控制台中将以下内容复制进去来定义molcyl绘图命令
proc molcyl {cenx ceny cenz axisx axisy axisz rad halfh} {
draw material Transparent
set startx [expr $cenx-$axisx*$halfh]
set starty [expr $ceny-$axisy*$halfh]
set startz [expr $cenz-$axisz*$halfh]
set start "$startx $starty $startz"
set endx [expr $cenx+$axisx*$halfh]
set endy [expr $ceny+$axisy*$halfh]
set endz [expr $cenz+$axisz*$halfh]
set end "$endx $endy $endz"
draw cylinder $start $end radius $rad filled yes resolution 40
}
然后利用molcyl命令就可以根据CYL的结果画出圆柱的图了,此命令的参数顺序是:柱中心XYZ坐标、轴矢量的XYZ分量、圆柱半径、圆柱半高。对于上例,我们输入molcyl 0.529569 0.669861 0.659797 0.996020 0.0491685 0.0743408 3.05604 14.3397之后就可以在屏幕上看到如下效果:

可见圆柱恰好套住了整个长链分子,所以CYL的结果是合理的。但要注意CYL给出的圆柱的参数没有把范德华半径考虑进去,而从图中可看到,与圆柱边缘相接的都是H,所以圆柱的半径和长度应当分别加上氢的范德华半径的一倍和二倍。
值得一提的是,长链体系往往具有很强柔性,不同构象下描述它的圆柱的参数可能有巨大差异,所以要注意说明是什么构象下计算的。
3 矩形盒子模型
一些体系适合矩形盒子模型,用长、宽、高来描述,比如下面的蒽,可以被矩形盒子很好扩住,比起圆球和圆柱模型都更合适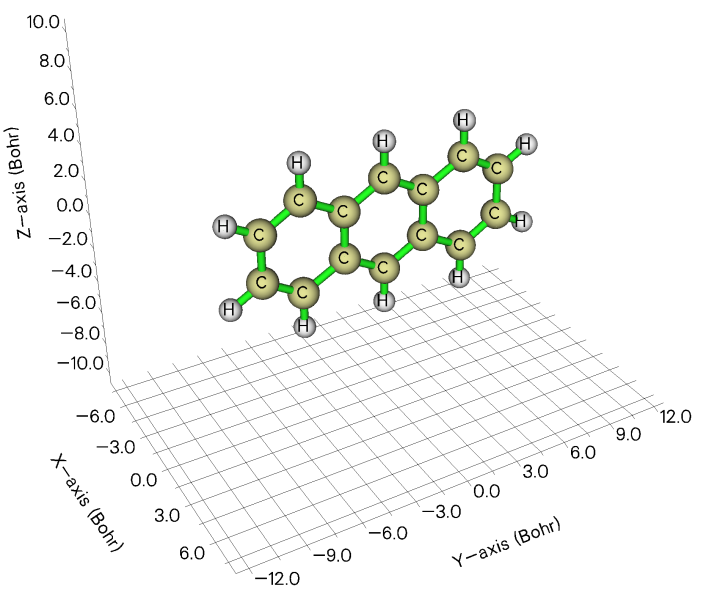
注:如果你的分子是复杂、歪斜的而非上图那么正,或者你想纯粹基于几何坐标快速计算长宽高,务必看后来写的《使用Multiwfn计算分子的长宽高》(http://sobereva.com/426)。
我们需要获得能够扩住这个分子范德华表面(这里用电子密度0.001等值面来定义)的最小盒子尺寸。这可以通过Multiwfn来做。先用Gaussian计算出这个分子的wfn或fch文件,载入进Multiwfn后选
12 //定量分子表面分析
2 //修改被映射的函数
-1 //改为用户自定义函数(计算没有耗时)
0 //开始分析
然后从屏幕的输出中能够找到ρ=0.001定义的分子表面的顶点的X、Y、Z方向上的最小和最大值:
Min-X: -2.0419 Max-X: 2.0420 Angstrom
Min-Y: -5.9055 Max-Y: 5.9055 Angstrom
Min-Z: -3.7916 Max-Z: 3.7916 Angstrom
比如盒子的Z长度就是3.7916*2=7.58埃。
我们可以用VMD来绘制出这个盒子。首先把以下内容复制到VMD的控制台里定义一个新命令drawbox
proc drawbox {xmin ymin zmin xmax ymax zmax} {
draw color blue
draw line " $xmin $ymin $zmin " " $xmax $ymin $zmin "
draw line " $xmin $ymin $zmin " " $xmin $ymax $zmin "
draw line " $xmax $ymin $zmin " " $xmax $ymax $zmin "
draw line " $xmin $ymax $zmin " " $xmax $ymax $zmin "
draw line " $xmin $ymin $zmax " " $xmax $ymin $zmax "
draw line " $xmin $ymin $zmax " " $xmin $ymax $zmax "
draw line " $xmax $ymin $zmax " " $xmax $ymax $zmax "
draw line " $xmin $ymax $zmax " " $xmax $ymax $zmax "
draw line " $xmin $ymin $zmin " " $xmin $ymin $zmax "
draw line " $xmin $ymax $zmin " " $xmin $ymax $zmax "
draw line " $xmax $ymin $zmin " " $xmax $ymin $zmax "
draw line " $xmax $ymax $zmin " " $xmax $ymax $zmax "
}
然后输入drawbox -2.0419 -5.9055 -3.7916 2.0420 5.9055 3.7916,就可以根据前面得到的数据绘制出相应的盒子。可见盒子能很好地扩住分子。
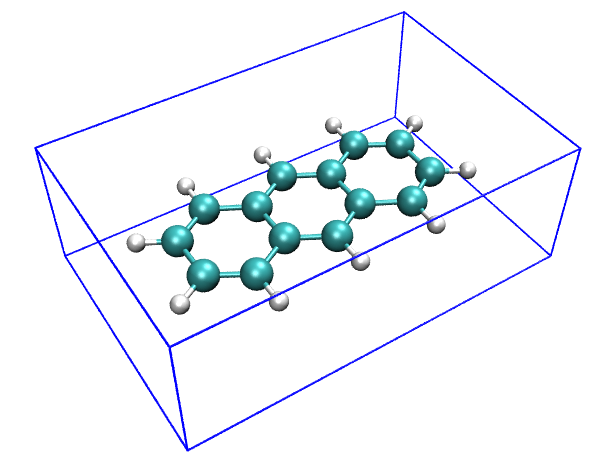
对于结构很复杂的体系,想要比较准确地且解析地描述它的形状,无论是圆球、圆片/圆柱或矩形盒子模型都已经不再适用,这种情况可以用球谐函数展开来表现,这在本文就不谈了。