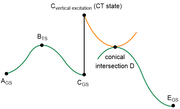Multiwfn forum

wham09

Member

Registered: 2025-09-19

Posts: 39

Miscellaneous questions on TDDFT/electron-hole analysis

Dear Prof. Lu,

I hope to get help with several questions on TDDFT calculation for electron-hole analysis.

1. For TDDFT, whether the functional is PBE0, LC-wPBE, CAM-B3LYP, or wB97XD, would you generally recommend DFT-D3(BJ)?

2. Is LC-wHPBE really superior to LC-wPBE as Gaussian advertises?

3. Can the same w-tuning procedure be applied whether the ground-state is singlet, doublet, or triplet, and whether it is neutral, anionic, or cationic?

4. Can electron excitation and a bond-formation or bond-cleavage reaction be concerted? Can it be calculated?

5. Is it more recommended (or not recommended) to do TD calculations with SMD rather than PCM?

6. For excited state optimization, can I just use nosymm keyword and skip the manual arbitrary breaking of symmetry?

7. For calculation of total Gibbs energy of an optimized excited state, please check if what I describe below seems correct:
  1) ES optimization (with GS checkpoint file available):
    wB97XD/def2-SVP   TD(Nstates=5, Root=2)   Opt   SCRF=solvent=dimethylsulfoxide   geom=modify   ...   geometry modification
  2) Take the structure and .chk file from 1). Run freq calculation:
    wB97XD/def2-SVP   TD(read, Nstates=5, Root=2)   Freq   SCRF=solvent=dimethylsulfoxide   guess=read
  3) Take the structure and .chk file from 1). Run SP calculation (gas-phase):
    wB97XD/def2-TZVP   TD(Nstates=5, Root=2)   guess=read
  4) Take the structure and .chk file from 1). Run SP calculation (gas-phase):
    M052X/6-31G*   TD(Nstates=5, Root=2)   guess=read
  5) Take the structure and .chk file from 1). Run SP calculation (solution-phase):
    M052X/6-31G*   TD(Nstates=5, Root=2)   SCRF=solvent=dimethylsulfoxide   guess=read
  6) Calculate E = E(step 3) + E(step 5) - E(step 4). Put it into Shermo and use .out file from step 2. Get thermal correction.

8. Suppose I have a reaction pathway A -> TS-1 -> B -> B* -> TS-2 -> C. The excited state B* is a charge-transfer state, for which I would want to use a long-range-corrected functional, such as CAM-B3LYP. But CAM-B3LYP would be less appropriate for calculation of other states A, B, TS-1, and TS-2. But then, for reaction coordinate energy calculations, shouldn't the functional be consistently used for every molecule from A to C?

9. For the TS-2 between B* and C in the question 8, am I looking for "excited state of transition state"? I don't know how to think about it.

sobereva

Tian Lu (Multiwfn developer)

From: Athens, Greece

Registered: 2017-09-11

Posts: 2,144

Website

Re: Miscellaneous questions on TDDFT/electron-hole analysis

1 DFT-D3(BJ) doesn't directly affect result of TDDFT

2 No

3 Can be

4 Electron excitation may directly cause or induce bond-formation or bond-cleavage. You can perform geometry optimization or calculate reaction path/barrier on excited state PES to verity the anticipation.

5 No. SMD doesn't have advantage in this regard.

6 No. If you geometry essentially has symmetry, even if you use "nosymm", the calculated atomic forces are still symmetric with respect to geometry.

7 It is too cumbersome. Simply use:
(1) wB97XD/def2SVP TD(Nstates=5,Root=2) opt freq SCRF(SMD,solvent=dimethylsulfoxide)
(2) wB97XD/def2TZVP TD(Nstates=5,Root=2) SCRF(SMD,solvent=dimethylsulfoxide) guess=read geom=allcheck
Set "E=" in settings.ini of Shermo to the 2nd excited state energy obtained from step (2), then boot up Shermo and load output file of step (1), you will obtain reasonable free energy of the 2nd excited state at its minimum.

8 CAM-B3LYP frequently overestimates excitation energy of local excitations. However, if your purpose is to explore reaction path over excited states, then CAM-B3LYP doesn't have well-known flaw.

9 If TS-2 is a transition state on excited state PES, you can certainly optimize it. Note that there may be no TS between B* to C, you may need to locate minimum energy conical intersection (MECI) to study the process (if you are not familiar with it, look at materials about computational photochemistry studies)

wham09

Member

Registered: 2025-09-19

Posts: 39

Re: Miscellaneous questions on TDDFT/electron-hole analysis

About question 1: To be more specific, after TD optimization is complete, and then if I want to run single-point calculation of the excited state to obtain total Gibbs free energy (following the procedure you suggested for the question 7), would you recommend DFT-D3(BJ) for the functionals I mentioned?

  About question 5: Just like question 1, for single-point calculation of the optimized excited state, SMD is preferred, right?

  About question 8: I guess the question was not specifically about CAM-B3LYP. For example, I could use LC-wPBE with w-tuning specific to the structure of B*. In this case, I thought that the specifically tuned LC-wPBE is probably not adequate for calculation of other ground states and transition states in the whole reaction path (which could be 10~20 steps), compared to more general functionals such as PBE0-D3(BJ) or B3LYP-D3(BJ). Is it okay to use a more general functional for non-excited states and compare their free energies with the free energy of B* calculated by tuned LC-wPBE?

  About question 9: I do have knowledge on conical intersections, although not an expert. My guess is perform relaxed scans (from the structure of B* to C) with 1) standard and 2) TD settings, and find out a scan point where the two energies are most similar? Could you let me know if there is a better, or a more appropriate, procedure?

sobereva

Tian Lu (Multiwfn developer)

From: Athens, Greece

Registered: 2017-09-11

Posts: 2,144

Website

Re: Miscellaneous questions on TDDFT/electron-hole analysis

About question 1: DFT-D3(BJ) correction is calculated fully based on geometry and irrelevant to electronic structure, therefore it affects geometry optimization process but doesn't directly affect vertical excitation energy. If you believe dispersion interaction notably affect geometry of your system, then adding DFT-D3(BJ) would be safer.

About question 5: The only advantage of SMD compared to the default IEFPCM is that the former explicitly considers non-polar contribution. This contribution doesn't directly affect excitation energy and electronic structure. If you hope the calculated energy of a given state includes full solvation energy (including non-polar contribution), then SMD is preferred over IEFPCM.

About question 8: As your purpose is not to accuractly calculate excitation energies, but reaction energies/barriers, w-tuned LC-wPBE doesn't have ANY advantage compared to many general functionals. Using wB97XD is recommended for both ground state and excited state reaction energies/barriers. PBE0-D3(BJ) or B3LYP-D3(BJ) cannot correctly represent evident CT state (even geometry)

About question 9: There are dedicated MECI optimization algorithms, see e.g.
Chem. Eur. J., 10, 2327 (2004)
Mol. Phys., 104, 1039 (2006)
JCTC, 6, 1538 (2010)
Gaussian can optimize MECI at CASSCF level, ORCA can optimize MECI at TDDFT and SF-TDDFT level.
Relaxed scan can rarely used to locate MECI.

wham09

Member

Registered: 2025-09-19

Posts: 39

Re: Miscellaneous questions on TDDFT/electron-hole analysis

question 8: From what I understood your comments, in the figure that I attached (green: non-excited PES, orange: excited PES), is it correct that calculating accurate relative Gibbs free energies of all 6 points under the same calculation level is not feasible?
  Especially because, for my specific molecule, the CT state of interest is assigned as the 2nd excited state when calculated with wB97XD, but is correctly (I think) assigned as the 1st excited state only when the w-tuned LC-wPBE is used.

question 9: Also related to question 8, if I optimize the MECI structure with CASSCF, is it possible to calculate its delta G relative to other states on the reaction path calculated by DFT methods?

Additional question about Q9: As I explained above, the CT state of my molecule is assigned differently depending on the functional. So I'm not confident that CASSCF will assign the CT state as the 1st excited state. Then, should I increase the number of electrons and orbitals in the active space to be safe?

Additional question (new): I would think that state-specific solvation of the vertical excitation state will affect vibrational frequencies differently (in principle) from the linear response. Can I do excited state freq calculation under this exact state-specific environment? Perhaps do TD=read from the state-specific solvated TD calculation chk?

Last edited by wham09 (2025-11-09 15:55:37)

sobereva

Tian Lu (Multiwfn developer)

From: Athens, Greece

Registered: 2017-09-11

Posts: 2,144

Website

Re: Miscellaneous questions on TDDFT/electron-hole analysis

8: It is impossible to calculate free energy at MECI and the fourth point, which are not stationary point on PES.

9: No.

Additional Q9: You can ask program to calculate larger number of roots, which is not directly related to increasing active orbitals/electrons.

(new): With state-specific solvation treatment, you don't have analytical derivatives, the cost of evaluating fully numerical Hessian is quite expensive (usually computationally prohibitively expensive).