Multiwfn forum

Aparna Gangwar

Member

Registered: 2025-08-16

Posts: 7

Calculation of Pauli potential using multiwfn

I have manually calculated the Pauli potential and electron density for atoms with spherically symmetric ground-state densities using data from Gaussian log files. To verify my results, I also attempted to calculate the Pauli potential using Multiwfn. I carefully followed the steps provided in the Multiwfn manual, but the values I obtained from the software do not match my manually calculated results.Could anyone please clarify the correct procedure for calculating the Pauli potential in Multiwfn?

sobereva

Tian Lu (Multiwfn developer)

From: Beijing

Registered: 2017-09-11

Posts: 2,055

Website

Re: Calculation of Pauli potential using multiwfn

Without description of your calculation steps in Multiwfn, it is difficult for me to make comment. I just tried, using Pauli potential (iuserfunc=53 with ispecial=0 or 1), to calculate grid data for Ar atom, the isosurface of Pauli potential is indeed fully spherically symmetric.

Aparna Gangwar

Member

Registered: 2025-08-16

Posts: 7

Re: Calculation of Pauli potential using multiwfn

I have used this information given below on page 39 multiwfn manual Multiwfn_3.8_dev.                                                                                                                                                      60 Pauli potential: V. Multiwfn supports two ways to evaluate this function, depending on
"ispecial" in settings.ini:
• ispecial=0: According to Eq. 17 of Comput. Theor. Chem., 1006, 92 (2013), V =  + VESP − VXC
− VW, where  is chemical potential (assumed to be zero by Multiwfn), VESP is electrostatic potential
(as described in Section 2.6) and VXC is exchange-correlation potential (its form is determined by
"iDFTxcsel" in settings.ini, see later).
• ispecial=1: Use original definition, namely ?θ = ?S − ?W = ??S
[?]/?? − ??W[?]/??, where VS is potential of non-interacting kinetic energy functional (S), and VW is potential of Weizsäcker
kinetic energy functional (vW). The form of S can be chosen by "iKEDsel" in settings.ini, see later;
currently only iKEDsel of 3, 5, 7 are supported

sobereva

Tian Lu (Multiwfn developer)

From: Beijing

Registered: 2017-09-11

Posts: 2,055

Website

Re: Calculation of Pauli potential using multiwfn

Using iuserfunc=60 is correct. But as I mentioned, I cannot reproduce your observation, at least for Ar atom... More detailed information, such as input file, all commands you inputted in Multiwfn, the result, should be given.

Aparna Gangwar

Member

Registered: 2025-08-16

Posts: 7

Re: Calculation of Pauli potential using multiwfn

%mem=90mw
%nprocs=23
%chk=Ar.chk
# HFS/6-31G output=wfn  Pop =full
gfinput gfoldprint iop(6/7=3)

title card

0 1
Ar     0.000000     0.000000     0.000000

Ar.wfn
This is the Gaussian input file I used to run my calculation. After that, I loaded the Ar.fchk file into Multiwfn. From the main menu, I selected option 3 (“Output and plot specific property in a line”). Then I chose option 100 (“User-defined function (iuserfunc = 60), see Section 2.7 of the manual”).

After this, the following prompt appeared:
0 Set extension distance for mode 1, current: 1.5000 Bohr
1 Input index of two atoms to define a line
2 Input coordinate of two points to define a line
At this stage, I selected option 2 and entered the x, y, and z coordinates as 0,0,0, 10,0,0.

sobereva

Tian Lu (Multiwfn developer)

From: Beijing

Registered: 2017-09-11

Posts: 2,055

Website

Re: Calculation of Pauli potential using multiwfn

In this way it is impossible to check if the Pauli potential is actually spherically symmetric. You should view isosurface map (via main function 5. Using isovalue of e.g. 0.7). You will find the isosurface is perfectly spherical.

Aparna Gangwar

Member

Registered: 2025-08-16

Posts: 7

Re: Calculation of Pauli potential using multiwfn

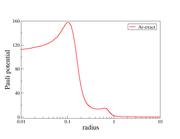
Thank you for the suggestion. However, my intention is not to check whether the Pauli potential is spherically symmetric or not. What I actually want is to calculate the Pauli potential of atoms and molecules and save its values along the radial direction.

sobereva

Tian Lu (Multiwfn developer)

From: Beijing

Registered: 2017-09-11

Posts: 2,055

Website

Re: Calculation of Pauli potential using multiwfn

In this case, your steps are correct.

Aparna Gangwar

Member

Registered: 2025-08-16

Posts: 7

Re: Calculation of Pauli potential using multiwfn

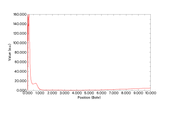
This is the Pauli potential graph I obtained by following the steps discussed above in Multiwfn. The other image I am attaching here corresponds to the Pauli potential obtained from my manual calculation. I would kindly request if you could try running the Pauli potential calculation for the Ar atom using the same procedure and share the results with me, so that I can cross-check my implementation.

sobereva

Tian Lu (Multiwfn developer)

From: Beijing

Registered: 2017-09-11

Posts: 2,055

Website

Re: Calculation of Pauli potential using multiwfn

This map is plotted for Ar calculated at B3LYP/6-31G* level using latest version of Multiwfn with iuserfunc=60, iDFTxcsel=84 and ispecial=0, the basic character is more close to your first image.

Aparna Gangwar

Member

Registered: 2025-08-16

Posts: 7

Re: Calculation of Pauli potential using multiwfn

Thank you very much for your reply and for sharing the details. I have followed the same method as you suggested and obtained almost the same graph. However, I observe negative values on the order of 10⁻⁴ near zero, along with some irregular behavior in that region.

If I want to change the number of grid points and the length of the radius, what is the correct way to do so? I suspect that increasing the number of grid points might help resolve this abnormality near zero.

Also, I apologize for these are very basic questions — I am quite new to using Multiwfn.

Last edited by Aparna Gangwar (2025-08-27 12:57:22)

sobereva

Tian Lu (Multiwfn developer)

From: Beijing

Registered: 2017-09-11

Posts: 2,055

Website

Re: Calculation of Pauli potential using multiwfn

Increasing number of grid point will not evidently affect the observed result.

Please take care of the calculation equation of Pauli potential used in Multiwfn (part 60 of Section 2.7 of Multiwfn manual). As you can see there are three component terms in the case of ispecial=0, you can individually plot them via Multiwfn to understand the detail. In which, Weizsacker potential (Vw) corresponds to iuserfunc=4, exchange-correlation potential (V_XC) corresponds to iuserfunc=1100.
BTW: Note that the position of nucleus is a singular point of the nuclear attractive potential in ESP, Multiwfn arbitrarily sets nuclear contribution to ESP at this point to 1000 a.u.

Because of approximations, such as approximated V_XC and finite-sized basis set, the resulting curve may not be well consistent with analyical solution.

Aparna Gangwar

Member

Registered: 2025-08-16

Posts: 7

Re: Calculation of Pauli potential using multiwfn

Thank you very much for the detailed explanation and for pointing me to the relevant section of the manual.